Question

A beam of light is converging towards a point on the screen. If a plane parallel plate of glass of refractive index$\mu $ and thickness t is introduced in the path of the beam, the convergent point is shifted
A. $t\left[ 1-\dfrac{1}{\mu } \right]$ away
B. $t\left[ 1+\dfrac{1}{\mu } \right]$ nearer
C. $t\left[ 1+\dfrac{1}{\mu } \right]$ away
D. $t\left[ 1-\dfrac{1}{\mu } \right]$ nearer

Answer 1

Hint: We could solve this problem by using simple geometry along with Snell’s law. First of all draw a neat diagram to see that the convergent point is shifted away on placing the plate. Now use trigonometric functions accordingly by considering appropriate triangles and also use the Snell’s law. Rearranging accordingly will give us the required shift.

Formula used:
Snell’s law,
$\dfrac{\sin i}{\sin r}=\mu $

Complete answer:
In the question, we are given a beam of light that converges towards some point on the screen. A shift in convergent point is observed when a parallel plate made of glass of refractive index $\mu $ and thickness t is introduced in the path of this beam. Let us represent the given situation in a diagram.

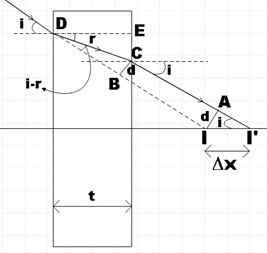
Consider the$\Delta DEC$,
$\cos r=\dfrac{DE}{DC}$
But from the figure, we see that DE is the thickness of the plate, so,
$\cos r=\dfrac{t}{DC}$
$\Rightarrow DC=\dfrac{t}{\cos r}$ ……………………………………. (1)
Now consider the$\Delta CBD$, here we see that,
$\sin \left( i-r \right)=\dfrac{BC}{DC}$
But BC is equal to d and by using (1),
$\sin \left( i-r \right)=\dfrac{d\cos r}{t}$
$\Rightarrow d=\dfrac{t\sin \left( i-r \right)}{\cos r}$
But we know the relation,
$\sin \left( a-b \right)=\sin a\cos b-\sin b\cos a$
$\Rightarrow d=\dfrac{t\left( \sin i\cos r-\sin r\cos i \right)}{\cos r}$
$\Rightarrow d=t\left( \sin i-\sin r\dfrac{\cos i}{\cos r} \right)$ ……………………………………………. (2)
Now let us consider the$\Delta AII'$, here we see that,
$\sin i=\dfrac{AI}{II'}$
But AI is equal to d and II’ is the path difference to be found,
$\sin i=\dfrac{d}{\Delta x}$
$\Rightarrow \Delta x=\dfrac{d}{\sin i}$
Substituting (2) we get,
$\Delta x=t\left( \dfrac{\sin i}{\sin i}-\dfrac{\sin i\cos i}{\sin i\cos r} \right)$
But from Snell’s law we know that,
$\dfrac{\sin i}{\sin r}=\mu $
$\Rightarrow \Delta x=t\left( 1-\dfrac{1}{\mu }\dfrac{\cos i}{\cos r} \right)$
On assuming near normal incidence we could say that the incident angle and the refracted angle are both really small. So,
$\cos i\approx \cos r\approx 1$
$\therefore \Delta x=t\left( 1-\dfrac{1}{\mu } \right)$
Also, we could clearly see from the diagram above that the convergent point is getting shifted away on placing the plate. So, we could say that, on introducing a plane parallel plate of glass of refractive index$\mu $ and thickness t in the path of the beam, the convergent point is shifted $t \left( 1-\dfrac{1}{\mu } \right)$ away.

Hence, option A is found to be the correct answer.

Note:
When we assume near normal incidence, we are actually assuming that the incident angle and the refracted angle are too small such that they can be very close to zero. And we know that the cosine of the zero is one. Hence, we have substituted for $\cos i$ and$\cos r$, thus, we got the final expression.