Question

A beam of a mixture of $ \alpha $ particles and protons are accelerated through the same potential difference before entering into the magnetic field of strength $ B $ . If $ {r_1} = 5cm $ , then $ {r_2} $ is

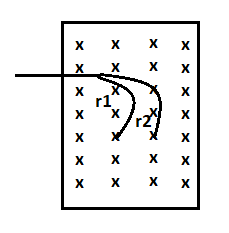
(A) $ 5\;cm $
(B) $ 5\sqrt 2 cm $
(C) $ 10\sqrt 2 cm $
(D) $ 20\;cm $

Answer 1

Hint: We know that both alpha particles and protons are charged particles. If a charged particle perpendicular to the uniform magnetic field. The magnetic Lorentz force is acting perpendicular to the velocity. This supplies the necessary centripetal force required for circular motion.

Formula used:
 $ v = \dfrac{{qBr}}{m} $
Where $ v $ is the velocity of the particle, $ q $ stands for the charge of the particle, $ B $ stands for the magnetic field, $ r $ is the radius of the circular path, and $ m $ is the mass of the particle.

Complete Step by step solution:
The velocity of a charged particle moving in a circular path in a uniform magnetic field is given by,
 $ v = \dfrac{{qBr}}{m} $
From this equation, we can write the expression for radius as,
 $ r = \dfrac{{mv}}{{qB}} $
We know that the momentum of the particle,
 $ P = mv $
Therefore, the radius can be written as
 $ r = \dfrac{P}{{qB}} $
We know that momentum can be written as,
 $ P = \sqrt {2mE} $
Substituting in the above equation, we get
 $ r = \dfrac{{\sqrt {2mE} }}{{qB}} $
We can write the energy of a charged particle in a potential $ V $ as,
 $ E = qV $
Substituting in the above equation, we get
 $ r = \dfrac{{\sqrt {2mqV} }}{{qB}} $
This equation can be rearranged as,
 $ r = \sqrt {\dfrac{m}{q}} \dfrac{{\sqrt {2V} }}{B} $
The radius $ {r_1} $ can be written as,
 $ {r_1} = \sqrt {\dfrac{{{m_1}}}{{{q_1}}}} \dfrac{{\sqrt {2V} }}{B} $
The radius $ {r_2} $ can be written as,
 $ {r_2} = \sqrt {\dfrac{{{m_2}}}{{{q_2}}}} \dfrac{{\sqrt {2V} }}{B} $
The ratio of the two radii can be written as,
 $ \dfrac{{{r_2}}}{{{r_1}}} = \dfrac{{\sqrt {\dfrac{{{m_2}}}{{{q_2}}}} \dfrac{{\sqrt {2V} }}{B}}}{{\sqrt {\dfrac{{{m_1}}}{{{q_1}}}} \dfrac{{\sqrt {2V} }}{B}}} $
Cancelling the common terms and rearranging, we get
 $ \dfrac{{{r_2}}}{{{r_1}}} = \sqrt {\dfrac{{{m_2}}}{{{q_2}}}} \times \sqrt {\dfrac{{{q_1}}}{{{m_1}}}} $
This can be written as,
 $ \dfrac{{{r_2}}}{{{r_1}}} = \sqrt {\dfrac{{{m_2}}}{{{m_1}}}} \times \sqrt {\dfrac{{{q_1}}}{{{q_2}}}} $
We know that the mass of an alpha particle is four times that of the mass of protons. i.e.
 $ {m_\alpha } = 4{m_p} $
Here $ {m_2} $ is the mass of the alpha particle and $ {m_p} $ is the mass of the proton.
Therefore we can write,
 $ \sqrt {\dfrac{{{m_2}}}{{{m_1}}}} = \sqrt {\dfrac{4}{1}} $
Also, the charge of alpha particles are two times that of the charge of protons, i.e.
 $ {q_\alpha } = 2{q_p} $
Here $ {q_2} $ is the charge of the alpha particle and $ {q_1} $ is the charge of the proton, then we can write
 $ {q_2} = 2{q_p} $
Then the ratio will be
 $ \sqrt {\dfrac{{{q_1}}}{{{q_2}}}} = \sqrt {\dfrac{1}{2}} $
Putting these values in the expression
 $ \dfrac{{{r_2}}}{{{r_1}}} = \sqrt {\dfrac{{{m_2}}}{{{m_1}}}} \times \sqrt {\dfrac{{{q_1}}}{{{q_2}}}} $
We get,
 $ \dfrac{{{r_2}}}{{{r_1}}} = \sqrt {\dfrac{4}{1}} \times \sqrt {\dfrac{1}{2}} = \sqrt 2 $
From this $ {r_2} = {r_1}\sqrt 2 $
It is given that, the value of $ {r_1} = 5cm $
Then,
 $ {r_2} = 5\sqrt 2 cm $
The answer is: Option (B): $ 5\sqrt 2 cm $ .

Note:
The radius $ r = \dfrac{{mv}}{{qB}} $ is known as the cyclotron radius. A cyclotron is a device employed to accelerate charged particles to high energies. It works on the principle that a charged particle moving normal to magnetic flux experiences magnetic Lorentz force. Because of this force, the particle moves in a circular path.