Question

A battery of internal resistance $3\Omega $ is connected to $20\Omega $ resistor and potential difference across the resistor is $10{\text{V}}$. If another resistor of $30\Omega $ is connected in series with the first resistor and battery is again connected to the combination, calculate the e.m.f and terminal potential difference across the combination.

Answer 1

Hint: If the resistors are connected in series then the net resistance is calculated differently and if the resistance is connected in parallel combination then the net resistance is calculated differently also the battery also has some internal resistance.

Complete answer:
As it is given that a battery is connected to a $20\Omega $ resistor having an internal resistance of $3\Omega $ and the potential difference across the resistor $20\Omega $ is $10{\text{V}}$. The $20\Omega $ resistor is connected in series with another resistor of $30\Omega $ and battery.
Here we need to find the value of e.m.f and the terminal potential difference across the combination.

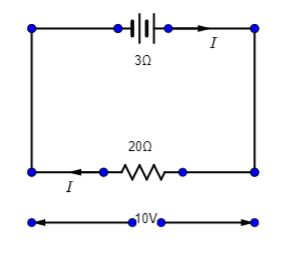
So first of all we will calculate the value of voltage across the resistor $20\Omega $.
$V = \left( {\dfrac{R}{{R + r}}} \right) \cdot E$ Where R is a resistor and r is internal resistance and E is the voltage. It is given that the potential difference is given as $10{\text{V}}$, the internal resistor is equal to $3\Omega $ and the resistor is $20\Omega $.
Therefore,
$ \Rightarrow V = \left( {\dfrac{R}{{R + r}}} \right) \cdot E$
$ \Rightarrow 10 = \left( {\dfrac{{20}}{{20 + 3}}} \right) \cdot E$
$ \Rightarrow 10 = \left( {\dfrac{{20}}{{23}}} \right) \cdot E$
$ \Rightarrow E = \left( {\dfrac{{230}}{{20}}} \right)$
$ \Rightarrow E = \left( {\dfrac{{23}}{2}} \right)$
$ \Rightarrow E = 11 \cdot 5{\text{V}}$
As the resistor of $20\Omega $ is connected with another resistor of $30\Omega $.

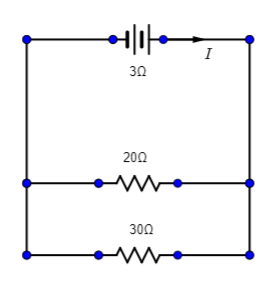
As the resistor of $20\Omega $ is connected with another resistor of $30\Omega $ and the battery with $3\Omega $ so the total resistance will be equal to,
$ \Rightarrow {R_{eq.}} = 20\Omega + 30\Omega + 3\Omega $
$ \Rightarrow {R_{eq.}} = 53\Omega $
According to the ohm’s law $V = I \cdot {R_{eq.}}$ where V is the voltage, I is the current and ${R_{eq.}}$ is the equivalent resistance.
The current in the circuit is given by,
$ \Rightarrow I = \dfrac{V}{{{R_{eq.}}}}$
$ \Rightarrow I = \dfrac{{11 \cdot 5}}{{53}}$
$ \Rightarrow I = 0 \cdot 22{\text{A}}$
The voltage difference across the combination is given by,
$ \Rightarrow V = I\left( {20 + 30} \right)$
As the current in the circuit is\[I = 0 \cdot 22{\text{A}}\].
$ \Rightarrow V = I\left( {20 + 30} \right)$
$ \Rightarrow V = \left( {0 \cdot 22} \right)\left( {20 + 30} \right)$
$ \Rightarrow V = \left( {0 \cdot 22} \right) \cdot \left( {50} \right)$
$ \Rightarrow V = 11{\text{Volts}}$
So the e.m.f is given by $E = 11 \cdot 5{\text{V}}$and the potential difference is given by $V = 11{\text{Volts}}$.

Note:
It is advisable for the students to remember the ohm's law. The way of solving the equivalent resistance is for the resistance connected in series or parallel. The battery does not just provide a potential difference it also has an internal resistance, while calculating the equivalent resistance always consider the internal resistance of the battery.