Question

A battery is connected between two pipes A and B on the circumference of a uniform conducting ring of radius r and resistance R. One of the arcs AB of the ring subtends an angle 0 at the centre. The value of the magnetic induction at the
centre due to the current in the ring is:
$A.\;{\text{proportional}}\;{\text{to}}\;{\text{2}}({\text{18}}{{\text{0}}^{\text{o}}}{\text{ - }}\theta )$
$B.\;{\text{inversely}}\;{\text{proportional}}\;{\text{to}}\;{\text{r}}$
$C.\;{\text{zero}}\;{\text{only}}\;{\text{if}}\;\theta {\text{ = 18}}{{\text{0}}^{\text{o}}}$
$D.\;{\text{zero}}\;{\text{for}}\;{\text{all}}\;{\text{values}}\;{\text{of}}\;\theta $

Answer 1

Hint: The magnetic field produced by a ring is proportional to the current. But the current in a wire is inversely proportional to the resistance of the wire. Also, we know that the resistance is proportional to the length of wire.

Complete Step by step answer
The correct answer is option D.
Batteries are constant voltage sources. The chemical reactions happening inside release a fixed voltage always. So if we connect it across a conducting ring as shown in the figure, the two segments would act as two parallel resistances connected across a cell.

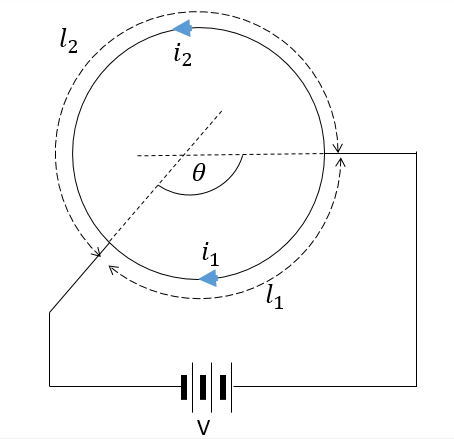
Now, as we know, when current passes through a circular wire, a magnetic field perpendicular to the plane of the wire is produced. The magnitude of this field is given by $B = \dfrac{{{\mu _0}i}}{{2\pi r}}$ and its direction can be found using the right-hand grip rule. Magnetic field due to a counterclockwise current looks like that of a North pole of a magnet and that of clockwise current looks like that of the south pole.
So A counterclockwise and clockwise current produces magnetic fields in opposite directions.
Here in the question, we have two segments of circle carrying currents. A circle is symmetric and hence, the total magnetic field at the center is proportional to the arc length.
The magnetic field due to a segment, which subtends $\theta $ angle at the center is $B = \dfrac{\theta }{{360}}\dfrac{{{\mu _0}i}}{{2\pi r}}$

But before proceeding further, we should remember that the current in the two parts of the ring is different. As both segments are of different lengths, their resistances would be different and hence a different current would flow through them.
Let's first find the resistances of the two segments so that we can find the currents.
If $\theta $ is the angle subtended by coil 1, then $360 - \theta $ is the angle subtended by coil 2. So their lengths can be given as:
${l_1} = \dfrac{\theta }{{360}}2\pi R$
${l_2} = \dfrac{{360 - \theta }}{{360}}2\pi R = \left( {\dfrac{{\theta '}}{{360}}} \right)2\pi R$ where $\theta ' = 360 - \theta $

We know that the resistance of a wire of given material is related to its length as :
$R = \dfrac{{\rho l}}{A}$
So the resistance of segments are :
${R_1} = \dfrac{{\rho {l_1}}}{A} = \dfrac{{\rho \left( {\dfrac{\theta }{{360}}2\pi R} \right)}}{A} = X\theta \;(say)$
\[{R_2} = \dfrac{{\rho {l_2}}}{A} = \dfrac{{\rho \left( {\dfrac{{\theta '}}{{360}}2\pi R} \right)}}{A} = X\theta '\]
Now since the two segments are across the same potential, we can use ohm’s law to find the currents.
Since $V = IR = $constant :
\[{I_1} = \dfrac{V}{{{R_1}}} = \dfrac{V}{{X\theta }}\] and \[{I_2} = \dfrac{V}{{{R_2}}} = \dfrac{V}{{X\theta '}}\]
Now that we know the currents, let us substitute this into equation(1) to find the Magnetic fields.

\[{B_1} = \dfrac{\theta }{{360}}\dfrac{{{\mu _0}{i_1}}}{{2\pi r}} = \dfrac{\theta }{{360}}\dfrac{{{\mu _0}\left( {\dfrac{V}{{X\theta }}} \right)}}{{2\pi r}} = \dfrac{{{\mu _0}V}}{{X2\pi r \times 360}}\]
\[{B_2} = \dfrac{{\theta '}}{{360}}\dfrac{{{\mu _0}{i_2}}}{{2\pi r}} = \dfrac{{\theta '}}{{360}}\dfrac{{{\mu _0}\left( {\dfrac{V}{{X\theta '}}} \right)}}{{2\pi r}} = \dfrac{{{\mu _0}V}}{{X2\pi r \times 360}}\]
So we see that both ${B_1}$ and ${B_2}$ have the same magnitude but opposite directions as one is clockwise and the other anticlockwise.
So the net magnetic field at the centre of the ring would be always zero independent of $\theta $.
Note: It would be better to remember this as a general result. The above result is true because the source of emf was a constant voltage source. Follow up questions with constant current source could be asked, where this result would not hold.