Question

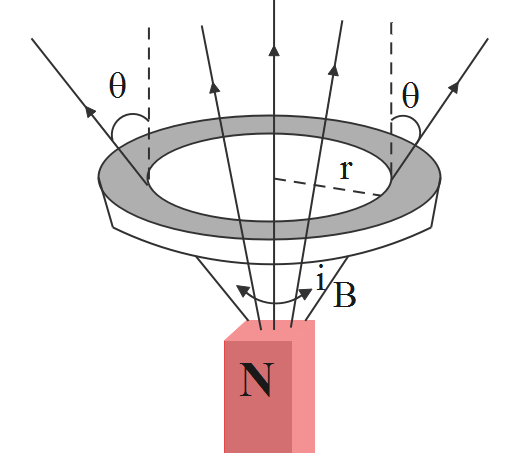
A bar magnet with its north pole up is placed along the axis of symmetry of a horizontal conducting ring carrying current I, as shown in the figure. At the location of the ring, the magnetic field makes an angle $\theta $ with the vertical. The mass of the ring is “m” and gravity acts vertically downwards. The ring stays in equilibrium, then the current passing through the ring is?

a.) $\dfrac{mg}{2\pi rB\sin \theta }$
b.) $\dfrac{mg}{\pi rB\sin \theta }$
c.) $\dfrac{2mg}{\pi rB\sin \theta }$
d.) $\dfrac{3mg}{2\pi rB\sin \theta }$

Answer 1

Hint: A magnet is an object or substance that generates a magnetic field. This magnetic field is invisible, but it is responsible for a magnet's most notable property: a force that attracts or repels other ferromagnetic materials such as iron, steel, nickel, cobalt, and others. A bar magnet is a rectangular piece of an object that has permanent magnetic properties and is made of iron, steel, or some other ferromagnetic material or ferromagnetic composite. It has two poles, one north and one south, and when suspended freely, the magnet aligns itself so that the northern pole faces the earth's magnetic north pole.

Complete answer:
In this question, we have been given that the mass of the ring is “m”
the magnetic field makes an angle $\theta $ with the vertical
Current in the conducting Ring = I
Equating the forces experienced by the ring
Force due to gravity = force due to magnetic field
$mg=IlB\sin \theta $
The length of the ring will be equal to its circumference and hence the length will be equal to
 $l=2\pi r$
Putting this value of length in the above equation we get
$mg=I(2\pi r)B\sin \theta $
$I=\dfrac{mg}{2\pi rB\sin \theta }$
This is the required value of current induced in the circuit
Hence, We can say that option (a) is the correct answer to this question.

Note:
Induced current is the current that is induced in a conducting loop that is subjected to a shifting magnetic field. The induced current's intensity will be determined by the changing magnetic flux. Consider Lenz's law, which states that an induced electric current can flow in such a way that it creates a magnetic field that opposes the change in the field that caused it, to determine the current's direction.