Question

A bar magnet is hung by a thin cotton thread in a uniform horizontal magnetic field and is in equilibrium state. The energy required to rotate it by ${{60}^{0}}$ is W. Now the torque required to keep the magnet in its new position is.
$\text{A}\text{. }\dfrac{2W}{\sqrt{3}}$
$\text{B}\text{. }\dfrac{W}{\sqrt{3}}$
$\text{C}\text{. }\sqrt{3}W$
$\text{D}\text{. }\dfrac{\sqrt{3}W}{2}$

Answer 1

Hint: To find the energy required to rotate the magnet by ${{60}^{0}}$ use the formula for work done, i.e. $W=\overrightarrow{M}.\overrightarrow{B}=MB\cos \theta $. Then use the formula of torque produced by the magnetic force, which is $\overrightarrow{\tau }=\overrightarrow{M}\times \overrightarrow{B}$.

Formula Used:
$W=\overrightarrow{M}.\overrightarrow{B}=MB\cos \theta $
$\overrightarrow{\tau }=\overrightarrow{M}\times \overrightarrow{B}$

Complete step-by-step answer:
It is given that a bar magnet is suspended in a horizontal uniform magnetic field.
When a bar magnet makes an angle $\theta $ with the magnetic field, the magnetic field apply a force on the which creates a torque on the bar magnet which is equal to $\overrightarrow{\tau }=\overrightarrow{M}\times \overrightarrow{B}$.
Here, B is the magnetic field and M is the magnetic moment of the bar magnet.
The magnitude of torque will be equal to $\tau =MB\sin \theta $.

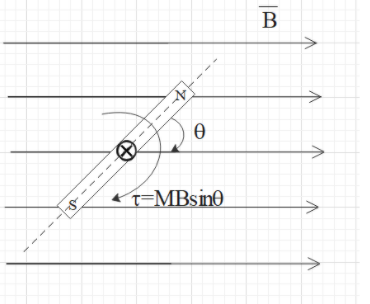
Now if we try to rotate the magnet about its midpoint, anti clockwise, then the magnetic force will apply force on the magnet that will oppose the motion of the magnet. Hence, we have to do work on the magnet equal to the work done by the electric force.
Work done by the magnetic field is $W=-\overrightarrow{M}.\overrightarrow{B}=-MB\cos \theta $.
Therefore, we have to do a work $W=\overrightarrow{M}.\overrightarrow{B}=MB\cos \theta $.
To do the work, W amount of energy is required.
It is given that $\theta ={{60}^{0}}$ and $\cos \theta =\cos 60=\dfrac{1}{2}$
Therefore, the energy needed to keep the magnet at ${{60}^{0}}$ is $W=\dfrac{MB}{2}$
Torque by the electric field on the magnet at ${{60}^{0}}$ will be $\tau =MB\sin 60=\dfrac{\sqrt{3}MB}{2}$.
But we found that $W=\dfrac{MB}{2}$.
Therefore, $\tau =\sqrt{3}W$
The torque required to keep the magnet in its new position is equal to $\sqrt{3}W$.
Hence, the correct option is C.

Note: Note that the net torque on the bar magnet at new position is zero because we are applying a torque equal and opposite to the torque applied by the magnetic force on the magnet so that it stays at rest.