Question

A bar magnet has been cut equally lengthwise and widthwise to give four equal pieces. The
pole strength of each piece as compared to the pole strength of original bar magnet is
A. Same
B. \[\dfrac{1}{8}\]
C. \[\dfrac{1}{4}\]
D. \[\dfrac{1}{2}\]

Answer 1

Hint: The bar magnet of length \[L\] and breadth \[B\] has to be cut into four equal pieces such that the length and breadth of these pieces are equal. Cutting the bar magnet parallel along the length and then perpendicularly along the length can only give four equal pieces such that the length of each piece is half the original length and the breadth of each piece is half the original breadth.

Formula Used: The pole strength of a magnet is: \[{q_m} = \dfrac{{{p_m}}}{L}\].

Complete step by step solution:
A magnetized bar is called a bar magnet. The ends of the bar magnet are called poles. The bar magnet is a dipole. The physical quantity representing the magnetization of the poles is called pole strength. It is denoted by \[{q_m}\]. The pole strength of the North Pole is positive and that of the South Pole is negative.The product of pole strength \[{q_m}\]and the length of the dipole \[L\] is called magnetic dipole moment \[{p_m}\]. Therefore, \[{q_m} = \dfrac{{{p_m}}}{L}\].

The magnetic dipole moment \[{p_m}\]depends upon the current (if any, through the coil wound on
magnet) and the area of cross section \[A\] of the magnet.Thus one can write \[{p_m} \propto A\]
The area of the magnet will be the length \[L\]times breadth \[B\] of the magnet. Thus, \[A = L \times B\]
Therefore, the pole strength of the bar magnet (without cutting) will be \[{q_m} \propto \dfrac{A}{L}
\propto \dfrac{{L \times B}}{L} \propto B\].

It is given in the diagram that magnet has been cut equally lengthwise and widthwise to give four equal
pieces. For this, one needs to cut the magnets parallel along the length such that the length remains the
same and the breadth is halved. Again, the magnet needs to be cut perpendicularly with the length, so
now the length is also halved. As a result, the four pieces will be equal. (See figure for reference).

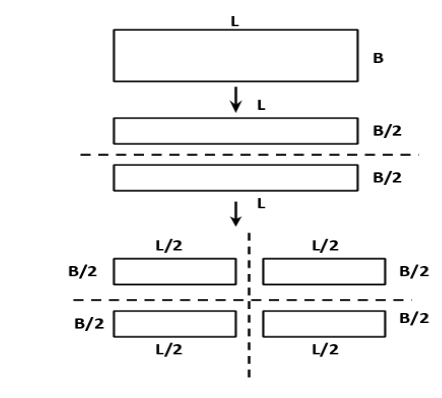
The pole strength of one of these pieces of magnet will be \[{q_m}^\prime \propto
\dfrac{{\dfrac{L}{2} \times \dfrac{B}{2}}}{{\dfrac{L}{2}}} \propto \dfrac{L}{2}\]
Therefore, the pole strength of each piece as compared to the pole strength of original bar magnet is
\[\dfrac{{{q_m}}}{{{q_m}^\prime }} = \dfrac{{\dfrac{L}{2}}}{L} = \dfrac{1}{2}\]

Hence, option (D) is the correct answer.

Note: After cutting the magnet, the north pole and the south pole remains the same, but the pole strength changes as it depends on the length and area of the magnet. The magnetization and the
magnetic moments are reduced such that each slices piece of the magnet is four times weaker than the
original magnet.