Question

A balloon descending at a constant acceleration\[\alpha \]. The mass of the balloon is M. When a mass m is released from the balloon; it starts rising with the same acceleration\[\alpha \]. Assuming that the volume does not change when the mass is released, what is the value of m?
A. \[\dfrac{\alpha }{{\alpha + g}}M\]
B. \[\dfrac{{2\alpha }}{{\alpha + g}}M\]
C. \[\dfrac{{\alpha + g}}{\alpha }M\]
D. \[\dfrac{{\alpha + g}}{{2\alpha }}M\]

Answer 1

Hint: In this question, we need to determine the mass of the balloon released in the surrounding so that the balloon could go up. For this, we will follow Newton's equations of motion by sketching a free body diagram of the given situation.

Complete step by step answer:
The mass of the balloon =M
Acceleration of descending\[ = \alpha \]
When the balloon is descending a constant acceleration\[\alpha \], a buyout force acts on it in the upward direction.
Let's draw a free body diagram of the balloon, which is descending a constant acceleration\[\alpha \].

'
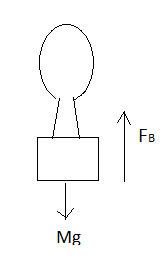Hence the equation of the force for the balloon while descending will be
\[Mg - {F_B} = Ma - - (i)\]
Now it is said that a mass m is released from the balloon due to which the balloon starts rising with the same acceleration\[\alpha \]
So the new mass of the balloon will be= M-m
When the balloon starts rising up then the buyout force will act in the downward direction, hence we get
\[{F_B} - \left( {M - m} \right)g = \left( {M - m} \right)a - - (ii)\]
Now we find the mass released by solving equation (i) and (ii)
Add equation (i) and (ii)
\[Mg - {F_B} + {F_B} - \left( {M - m} \right)g = M\alpha + \left( {M - m} \right)\alpha \]
Hence by further solving we get
$Mg - {F_B} + {F_B} - \left( {M - m} \right)g = M\alpha + \left( {M - m} \right)\alpha \\ $
$\implies Mg - Mg + mg = M\alpha + M\alpha - m\alpha \\ $
$ \implies mg = M\alpha + M\alpha - m\alpha \\ $
$\implies mg + m\alpha = 2M\alpha \\ $
$\implies m\left( {g + \alpha } \right) = 2M\alpha \\ $
$\therefore m = \dfrac{{2M\alpha }}{{\left( {g + \alpha } \right)}} \\ $
Hence the amount of mass m released from the balloon is equal to
$m = \dfrac{{2\alpha }}{{\left( {g + \alpha } \right)}}M $

So, the correct answer is “Option B”.

Note:
Students must note that whenever an object or the balloon is descending a buyout force acts on the balloon in the upward direction and when the balloon rises up then the buyout force acts in the upward direction.