Question

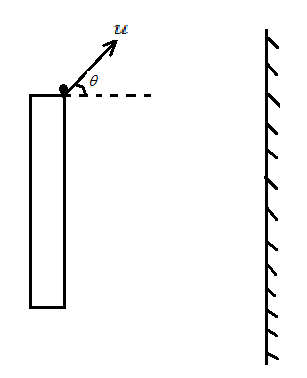
A ball is projected from top of the table with initial speed $ u $ at an angle of inclination $ \theta $ , motion of the image of the ball with respect to ball is:
(A) Must be projectile
(B) Must be straight line and vertical
(C) Must be straight line and horizontal
(D) Must be straight line depends upon value of $ \theta $

Answer 1

Hint :We have been given the diagram of the object and a mirror placed in front of it. The object is projected from the top of the table with initial velocity $ u $ . We must know that the image formed of any object in front of the mirror at some distance will give the image at the same distance behind the mirror. We have to resolve the components of $ u $ .

Complete Step By Step Answer:
First of all we know that the mirror image of any object is always formed behind the plane mirror and the velocity of the object is to be resolved as horizontal component along $ x $ axis is $ u\cos \theta $ and vertical component along $ y $ is $ u\sin \theta $ as shown in the figure below:

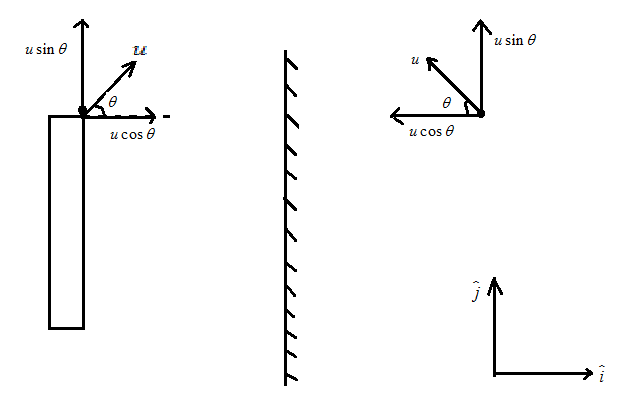
Let velocity of image with respect to object be $ \overrightarrow {{V_{IO}}} $ , velocity of object be $ \overrightarrow {{V_O}} $ and velocity of image be $ \overrightarrow {{V_I}} $
Therefore, we have
 $ \overrightarrow {{V_{IO}}} = \overrightarrow {{V_I}} - \overrightarrow {{V_O}} $ …… $ (1) $
From the above image we have resolved the components as
 $ \overrightarrow {{V_I}} = - u\cos \theta \widehat i + u\sin \theta \widehat j $ and $ \overrightarrow {{V_O}} = u\cos \theta \widehat i + u\sin \theta \widehat j $
 $ eq(1) \Rightarrow \overrightarrow {{V_{IO}}} = - u\cos \theta \widehat i + u\sin \theta \widehat j - (u\cos \theta \widehat i + u\sin \theta \widehat j) $
 $ \Rightarrow \overrightarrow {{V_{IO}}} = - 2u\cos \theta \widehat i + u\sin \theta \widehat j - u\sin \theta \widehat j $
 $ \Rightarrow \overrightarrow {{V_{IO}}} = - 2u\cos \theta \widehat i $
Thus, the velocity of the image is along a negative $ x $ direction.
Therefore the image will move in a straight line and horizontally in the opposite direction.
The correct answer is option C.

Note :
Here, it is necessary to resolve the components of velocity as we have done in the above answer and in figure we have given the components of $ x $ and $ y $ direction. And also remember that the mirror image in a plane mirror is the same as the object.