Question

A ball is let to fall from a height ${h_s}$ . It makes $n$ collisions with the horizontal ground. If after $n$ collisions it rebounds with a velocity ${v_a}$ and rises to a height ${h_a}$ then find the coefficient of restitution for the collision.

Answer 1

Hint:The coefficient of restitution refers to the ratio of the relative velocity of separation of the ground and the ball to their relative velocity of approach. After colliding with the ground, the ball rises to some height with some velocity and it will fall from that height with the same velocity. The mechanical energy of the system before and after the collision will be conserved.

Formulas used:
->The potential energy of a body at a height $h$ from the ground is given by, $PE = mgh$ where $m$ is the mass of the body and $g$ is the acceleration due to gravity.
->The kinetic energy of a body is given by, $KE = \dfrac{1}{2}m{v^2}$ where $m$ is the mass of the body and $v$ is the velocity of the body.
->The coefficient of restitution is given by, $e = \dfrac{{{v_{sep}}}}{{{v_{app}}}}$ where ${v_{sep}}$ and ${v_{app}}$ are the relative velocity of separation of two bodies and their relative velocity of approach respectively.

Complete step-by-step solution:
->Step 1: Sketch a figure depicting the collisions of the ball with the ground.

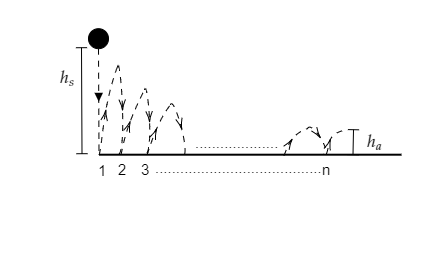
In the above figure, we see that the ball falls from the height ${h_s}$ , hits the ground and rises again to reach a smaller height. This refers to the first collision of the ball. The ball then falls from the smaller height, hits the ground and rises to reach an even smaller height. This is referred to as the second collision. This repeats $n$ times giving rise to $n$ collisions.
The height from the ground to which the ball rises after colliding with the ground for the $n{\text{th}}$ time is given to be ${h_a}$ .
Let ${v_0}$ be the velocity of the ball when it falls from ${h_s}$ .
Let ${v_1},{v_2},{v_3},......{v_{n - 1}},{v_a}$ be the velocities of the rising and falling of the ball after the collision 1, collision 2, collision 3, .…........, collision $\left( {n - 1} \right)$ and collision $n$ respectively.

->Step 2: Express the product of the coefficient of restitution of the collisions.
The coefficient of restitution is given by, $e = \dfrac{{{v_{sep}}}}{{{v_{app}}}}$ where ${v_{sep}}$ and ${v_{app}}$ are the relative velocity of separation of two bodies and their relative velocity of approach respectively.
For the first collision, the relative velocity of approach is ${v_0}$ and the relative velocity of separation is ${v_1}$ .
For the second collision, the relative velocity of approach is ${v_1}$ and the relative velocity of separation is ${v_2}$ .
This can be obtained for all the collisions.
Finally, for the $n{\text{th}}$ collision, the relative velocity of approach is ${v_{n - 1}}$ and the relative velocity of separation is ${v_a}$ .
So the coefficient of restitution for the first collision will be $e = \dfrac{{{v_1}}}{{{v_0}}}$ . Similarly, for the second collision we have $e = \dfrac{{{v_2}}}{{{v_1}}}$ .
Thus the coefficient of restitution for all the $n$ collisions will be $e = \dfrac{{{v_1}}}{{{v_0}}}$ , $e = \dfrac{{{v_2}}}{{{v_1}}}$ , $e = \dfrac{{{v_3}}}{{{v_2}}}$ , …………….., $e = \dfrac{{{v_{n - 1}}}}{{{v_{n - 2}}}}$, $e = \dfrac{{{v_a}}}{{{v_{n - 1}}}}$
Then the product of these coefficients will be ${e^n} = \dfrac{{{v_1}}}{{{v_0}}} \times \dfrac{{{v_2}}}{{{v_1}}} \times \dfrac{{{v_3}}}{{{v_2}}} \times ........... \times \dfrac{{{v_{n - 1}}}}{{{v_{n - 2}}}} \times \dfrac{{{v_a}}}{{{v_{n - 1}}}}$
Simplifying the above equation we get, ${e^n} = \dfrac{{{v_a}}}{{{v_0}}}$ -------- (1)

->Step 3: Based on the conservation of energy, express ${v_0}$ and ${v_a}$ .
The mechanical energy of the system is conserved. So the potential energy of the ball before the fall and its kinetic energy on reaching the ground will be equal.
i.e., $PE = KE$ ------- (2)
The potential energy of the ball at the height ${h_s}$ from the ground is given by, $PE = mg{h_s}$ and its kinetic energy on reaching the ground will be $KE = \dfrac{1}{2}m{v_0}^2$
Then from equation (2), we have $mg{h_s} = \dfrac{1}{2}m{v_0}^2$
$ \Rightarrow {v_0} = \sqrt {2g{h_s}} $
Similarly, the potential energy of the ball at the height ${h_a}$ from the ground is given by, $PE = mg{h_a}$ and the kinetic energy on reaching the ground will be $KE = \dfrac{1}{2}m{v_a}^2$
Then from equation (2), we have $mg{h_a} = \dfrac{1}{2}m{v_a}^2$
$ \Rightarrow {v_a} = \sqrt {2g{h_a}} $
Substituting for ${v_0} = \sqrt {2g{h_s}} $ and ${v_a} = \sqrt {2g{h_a}} $ in equation (1) we get, ${e^n} = \dfrac{{\sqrt {2g{h_a}} }}{{\sqrt {2g{h_s}} }} = \sqrt {\dfrac{{{h_a}}}{{{h_s}}}} $
Thus the coefficient of restitution will be $e = \sqrt[n]{{\dfrac{{{h_a}}}{{{h_s}}}}}$

Note:- The relative velocity of approach (or separation) is actually the difference between the velocities of the ball and the ground. But as the ground remains stationary, the velocity of approach (or separation) becomes the velocity of the ball itself. As the ball falls from a certain height its potential energy gets completely converted to kinetic energy on reaching the ground. The collision of the ball with the ground will change its velocity.