Question

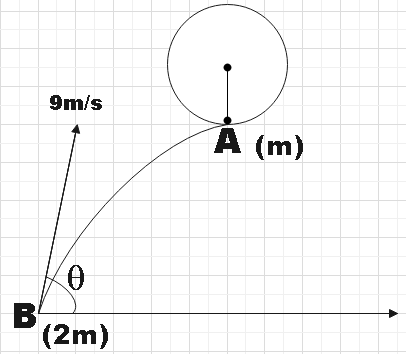
A ball A of mass m is suspended by a thread of length r=1.2m. Another ball B of mass 2m is projected from the ground with velocity $u=9m{{s}^{-1}}$ such that at the highest point of its trajectory it collides head on elastically with ball A. It is observed that during subsequent motion, tension in the thread at the highest point is equal to mg. The height of the point of suspension of ball A from the ground is:

A. $\dfrac{81}{40}m$
B. $\dfrac{129}{40}m$
C.$\dfrac{81}{20}m$
D. $\dfrac{101}{40}m$

Answer 1

Hint: Firstly, you could make a free body diagram of the ball A and then balance the forces acting on it to get its centripetal velocity. Then you could apply the law of conservation of energy and momentum to find the velocity of $A$ and $B$ after collision respectively. Then you could use the expression for COR to get the angle of the projectile and thus find the angle of projectile. The sum of the height and the length of the thread will give the answer.

Formula used:
Maximum height of projectile,
$H=\dfrac{{{\left( u\sin \theta \right)}^{2}}}{2g}$

Complete Step by step solution:
Let us take the velocity of ball A to be v at the highest point and then let us consider the free body diagram at that particular point.

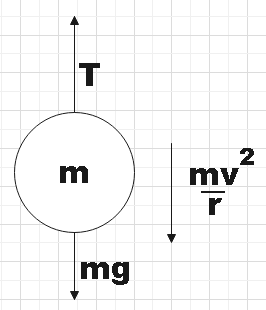
$\dfrac{m{{v}^{2}}}{r}-T=mg$
But we know that,
$T=mg$
$\Rightarrow {{v}^{2}}=2rg$
$\Rightarrow v=\sqrt{2rg}$

Substituting the values we get,
$\therefore v=2\sqrt{6}m{{s}^{-1}}$

Now let v’ be the velocity of ball A after the collision, then, on applying the law of conservation of energy we get,
$\dfrac{1}{2}mv{{'}^{2}}=\dfrac{1}{2}m{{v}^{2}}+mg\left( 2r \right)$
$\Rightarrow v'=\sqrt{6rg}$
$\therefore v'=6\sqrt{2}m{{s}^{-1}}$

Let the angle of projection of ball B be $\theta $, then the horizontal component of the velocity will be $9\cos \theta $ and we know that for a projectile motion, the horizontal velocity remains constant.

Now let the velocities of ball A and B be v’ and v” respectively. Then, from the law of conservation of momentum we have,
$mv'+2mv''=2m\left( 9\cos \theta \right)$ ……………………………………….. (1)

The coefficient of restitution for elastic collision is 1. So,
$e=\dfrac{v'-v''}{9\cos \theta }=1$
$\Rightarrow \left( v'-v'' \right)=9\cos \theta $ …………………………………………… (2)

Now let us solve the equations (1) and (2) to get,
$\cos \theta =\dfrac{1}{\sqrt{2}}$
$\therefore \theta =45{}^\circ $
Also, $v''=\dfrac{3}{\sqrt{2}}m{{s}^{-1}}$

We know that the height at which the initial position of ball A is the same as the maximum height of the projectile of ball B, that is,
$H=\dfrac{{{\left( 9\sin \theta \right)}^{2}}}{2g}=\dfrac{81}{40}m$

Therefore, the height of the point of suspension will be the sum of the height and the length of the thread. That is,
$H+r=\dfrac{81}{40}+1.2=\dfrac{81+48}{40}=\dfrac{129}{40}m$

Therefore, we found the height of the point of suspension of ball A from the ground to be$\dfrac{129}{49}m$.

Hence, option B is found to be the correct answer.

Note:
Some of the important points that we used in this solution that is always handy for solving questions similar to this are: (1) Horizontal velocity of a projectile is always constant. (2) The coefficient of restitution for an elastic collision is taken as 1. Also, for free body diagrams, always be careful about the direction.