Question

A and B are two points on a uniform ring of resistance $R$. The $\angle ACB=\theta $, where C is the centre of the ring. The equivalent resistance between A and B is:
(A). $\dfrac{R\theta (2\pi -\theta )}{4{{\pi }^{2}}}$
(B). $R\left( 1-\dfrac{\theta }{2\pi } \right)$
(C). $\dfrac{R\theta }{2\pi }$
(D). $\dfrac{R\theta (2\pi -\theta )}{4\pi }$

Answer 1

Hint: A ring has uniform resistance as we divide the ring into parts by the points A and B, its length changes and hence its resistance depends on the length. Calculating resistance per unit length, we can use it to calculate the resistance of an individual part of the ring. Apply the right combination to the resistance and calculate the equivalent resistance accordingly.
Formulas used:
$R'=\dfrac{R}{2\pi r}$
$R''=\dfrac{{{R}_{1}}\times {{R}_{2}}}{{{R}_{1}}+{{R}_{2}}}$

Complete step-by-step solution:

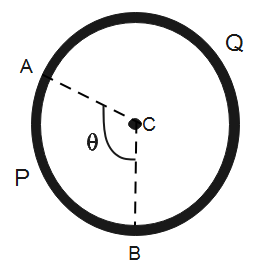
Given that the ring has a uniform resistance $R$. Let $r$ be the radius of the ring, then the resistance per unit length will be-
$R'=\dfrac{R}{2\pi r}$ - (1)
Here, $R'$ is the resistance per unit length of the ring
$2\pi r$ is the circumference or total length of the ring
The length of the arc APB will be-
$l=r\theta $ - (2)
Here, $\theta $ is the given angle $\angle ACB$
The length of the arc AQB will be-
$l'=r(2\pi -\theta )$ - (3)
The resistance of each arc will be the product of length of arc and the resistance per unit length. Therefore, the resistance of APB will be-
$\begin{align}
  & {{R}_{1}}=\dfrac{R}{2\pi r}\times r\theta \\
 & \Rightarrow {{R}_{1}}=\dfrac{R\theta }{2\pi } \\
\end{align}$
Therefore, the resistance of APB will be $\dfrac{R\theta }{2\pi }$.
From eq (1) and eq (3), the resistance of AQB will be-
$\begin{align}
  & {{R}_{2}}=\dfrac{R}{2\pi r}r(2\pi -\theta ) \\
 & \Rightarrow {{R}_{2}}=\dfrac{R(2\pi -\theta )}{2\pi } \\
\end{align}$
Therefore, the resistance of AQB will be $\dfrac{R(2\pi -\theta )}{2\pi }$.
Both arcs APB and AQB are connected between two points AB and hence are connected in parallel. Therefore, their equivalent resistance will be-
$R''=\dfrac{{{R}_{1}}\times {{R}_{2}}}{{{R}_{1}}+{{R}_{2}}}$
Substituting the value of ${{R}_{1}}$ and ${{R}_{2}}$ in the above equation, we get,
$\begin{align}
  & R''=\dfrac{\dfrac{R\theta }{2\pi }\times \dfrac{R(2\pi -\theta )}{2\pi }}{\dfrac{R\theta }{2\pi }+\dfrac{R(2\pi -\theta )}{2\pi }} \\
 & \Rightarrow R''=\dfrac{R\theta (2\pi -\theta )}{4{{\pi }^{2}}} \\
\end{align}$
Therefore, the equivalent resistance between points A and B is $\dfrac{R\theta (2\pi -\theta )}{4{{\pi }^{2}}}$. Hence, the correct option is (A).

Note: In parallel combination, the voltage is the same. For resistors connected in parallel, the inverse of equivalent resistance is equal to the sum of inverse of all resistances. The resistance of a material is inversely proportional to its area of cross section and directly proportional to its length.