Question

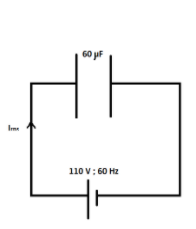
A $60\mu F$ capacitor is connected to a 110 V, 60 Hz a.c. supply. Determine the r.m.s value of current in the circuit.

Answer 1

Hint: RMS value mentioned in the question refers to the root mean square values (effective values). The given voltage can be considered as its rms value. Then using ohm’s law, we can calculate the rms value of current. As no resistor is connected, the resistance to the flow of current will be provided by the capacitor only.

Complete Step by step answer: Given:
Capacitance (C) of the capacitor = $60\mu F = 6 \times {10^6}F\left( {\because 1F = {{10}^6}\mu F} \right)$
Root mean square value of voltage = 110 V
Frequency $\left( \nu \right)$ = 60 Hz.

Now, according to ohm’s law:
V = IR but here we are considering root mean square values of both voltage and current, so:
$
  {V_{rms}} = {I_{rms}}R \\
   \Rightarrow {I_{rms}} = \dfrac{{{V_{rms}}}}{R}......(1) \\
 $
Because we need to calculate the r.m.s value of current.
In the circuit, there is no resistor connected. So the net resistance only be provided by the capacitor known as capacitive reactance which is given as:
$
  {X_C} = \dfrac{1}{{\omega C}} \\
  \Rightarrow {X_C} = \dfrac{1}{{2\pi \nu C}}\left( {\because \omega = 2\pi \nu } \right) \\
 $
Substituting the given values of frequency and capacitance, we get:
$
  {X_C} = \dfrac{1}{{2\pi \nu C}} \\
 \Rightarrow {X_C} = \dfrac{1}{{2 \times 3.14 \times 60 \times 60 \times {{10}^{ - 6}}}} \\
   \Rightarrow {X_C} = 44.2\Omega \\
 $
As this is the resistance provided by to the flow of current, its SI unit will be ohms $\left( \Omega \right)$
Equation (1) becomes:
${I_{rms}} = \dfrac{{{V_{rms}}}}{{{X_C}}}$
Substituting all the known values, we get:
$
  {I_{rms}} = \left( {\dfrac{{110}}{{44.2}}} \right)A \\
  \Rightarrow {I_{rms}} = 2.49A \\
 $
Therefore, the r.m.s value of current in the circuit is 2.49 Amperes.

Note: Root mean square value is known as effective or virtual value of alternating current (AC). the amount of heating effect produced is equivalent to that produced by direct current (DC) Important SI Units of different quantities are:
Capacitance – Faraday (F), Voltage – Volts (V), Resistance – Ohm’s $\left( \Omega \right)$ , Frequency – Hertz (Hz) and Current – Ampere (A)
From the units only, we can get an idea about the quantity which is talked about in the question.