Question

A 600pF capacitor is charged by a 200V supply. It is then disconnected from the supply and is connected to another uncharged 600pF capacitor. How much electrostatic energy is lost in the process?

Answer 1

Hint: Here the capacitor gets charged first and then gets discharged when connected to another uncharged capacitor. Thus there is loss in energy. Here the capacitors are connected in series. We know that the energy of the capacitor is $E=\dfrac{1}{2}CV^{2}$

Formula used: the energy of the capacitor is $E=\dfrac{1}{2}CV^{2}$
$\dfrac{1}{C_{net}}=\dfrac{1}{C}+\dfrac{1}{C}$

Complete step-by-step solution -
A capacitor is a two terminal component that stores electrical energy, and later discharges them. This property is called the capacitance of the capacitor.
We know that the energy of the capacitor is $E=\dfrac{1}{2}CV^{2}$ ,where $C$ is the capacitor and $V$ is the potential difference.

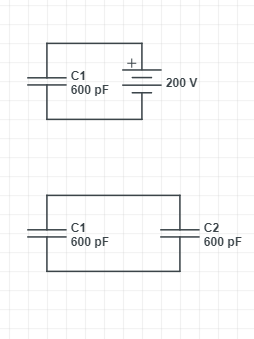
Here $C=600pF$ and $V=200V$
Then $E=\dfrac{1}{2}\times(600\times 10^{-12})\times(200)^{2}$
$E=1.2\times 10^{-5} J$

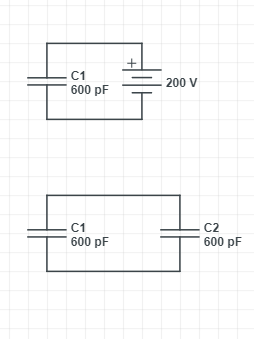
When the capacitor is disconnected and connected to the uncharged capacitor, the net capacitance $\dfrac{1}{C_{net}}=\dfrac{1}{C}+\dfrac{1}{C}=\dfrac{1}{600}+\dfrac{1}{600}=\dfrac{2}{600}=\dfrac{1}{300}$
$C_{net}=300pF$
Then the new energy is given by $E\prime=\dfrac{1}{2}C_{net}V^{2}$
 $E\prime=\dfrac{1}{2}\times (300\times 10^{-12})\times(200)^{2}$
$E\prime=0.6\times 10^{-5} J$
The difference in energy is $=E-E\prime$
$=1.2\times 10^{-5}- 0.6\times 10^{-5}=0.6\times 10^{-5}=6\times 10^{-6}J$
Therefore the loss of energy is $6\times 10^{-6}J$

Additional Information:
A capacitor can store electrical energy, and behaves as a temporary battery. They are used mainly to maintain the power supply while batteries are being changed. It can also store information in the form of binary digits. It is the main component used in full wave and half wave rectifiers. SI unit of capacitor is farad (symbol: F), named after the English physicist Michael Faraday. A 1 farad capacitor, when charged with 1 coulomb of electrical charge, has a potential difference of 1 volt between its plates. The series of capacitors is the sum of reciprocal of its individual capacitors, whereas in resistance the parallel is the sum of reciprocal of its individual resistors. Also remember that capacitors can charge and discharge.

Note: The series of capacitors is the sum of reciprocal of its individual capacitors, whereas in resistance the parallel is the sum of reciprocal of its individual resistors. Also remember that capacitors can charge and discharge.