Question

A 2m ladder leans against a vertical wall. If the top of the ladder begins to slide down the wall at the rate 25 cm/sec, then the rate (in cm/sec.) at which the bottom of the ladder slides away from the wall on the horizontal ground when the top of the ladder is 1m above the ground is?\[\]
A.$25\sqrt{3}$\[\]
B. $25$\[\]
C. $\dfrac{25}{\sqrt{3}}$\[\]
D. $\dfrac{25}{3}$\[\]

Answer 1

Hint: Draw a diagram of the ladder inclined on the wall. Assign the variables for changing distances and use Pythagoras theorem. Design a differential equation and put all the values given in the question.

Complete step by step answer:

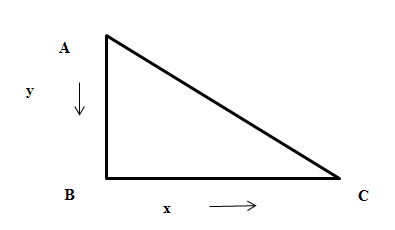
We can see in the figure that the initial position of the ladder of length 2m was AC where A is top of the ladder and C is the bottom of the ladder. As the top of the ladder A slides downwards vertically the bottom of the ladder slides rightwards horizontally .\[\]
 Let us assign the varying the vertical distance of the top the ladder from the ground as $y$ ,the varying horizontal distance of the bottom of the ladder from the wall as $x$ and varying time as $t$ . At any point during the slide the ladder will make a right-angled triangle with the wall. Using Pythagoras theorem where the ladder is hypotenuse,
\[{{x}^{2}}+{{y}^{2}}={{2}^{2}}=4...\left( 1 \right)\]
Differentiating the above equation with respect to $t$ we proceed,
\[\begin{align}
& 2x\dfrac{dx}{dt}+2y\dfrac{dy}{dt}=0 \\
& \Rightarrow x\dfrac{dx}{dt}+y\dfrac{dy}{dt}=0..\left( 2 \right) \\
\end{align}\]
Where $\dfrac{dx}{dt}$ is the rate of change in horizontal distance and $\dfrac{dy}{dt}$ is rate of change in vertical distance. As given the question $\dfrac{dy}{dt}=-25$ cm/sec. We have been asked to find the value when the vertical distance $y=1$ m. Using the Pythagoras theorem to find the horizontal distance at $y=1$ we get $x={{2}^{2}}-{{1}^{2}}=\sqrt{3}$ . Putting all these values in equation (2) we proceed,
\[\begin{align}
& \Rightarrow x\dfrac{dx}{dt}+y\dfrac{dy}{dt}=0 \\
& \Rightarrow \left( \sqrt{3} \right)\dfrac{dx}{dt}+1\left( -25 \right)=0 \\
& \Rightarrow\dfrac{dx}{dt}=\dfrac{25}{\sqrt{3}} \\
\end{align}\]
So the ladder slides away from the wall at a rate of $\dfrac{25}{\sqrt{3}}$ cm/sec.

The correct choice is C.

Note: The question tests your knowledge of application of differential calculus and Pythagoras theorem. Careful solution of simultaneous equation and use of formula will help you to arrive at the correct result. The question can be framed to find the rate of sliding down with the rate of sliding away given in the question.