Question

$ A = (2,2),\,\,B = (2,5)\,\,and\,\,C(5,2) $ form a triangle. The circumcentre of $ \Delta ABC $ is
 $
  A.\,\,\left( {3,3} \right) \\
  B.\,\,\left( {2,2} \right) \\
  C.\,\,\left( {3.5,3.5} \right) \\
  D.\,\,\left( {2.5,2.5} \right) \\
  $

Answer 1

Hint: To find circumcentre we first let centre of a circle as (a, b) then finding radius OA, OB and OC by using distance formula and then equating them in pair to form two equations and then on solving them we get value of ‘a’ and ‘b’ and hence circumcentre of the given triangle.
Distance between two points: $ \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} $

Complete step-by-step answer:
Let (a,b) be the radius of the circle.

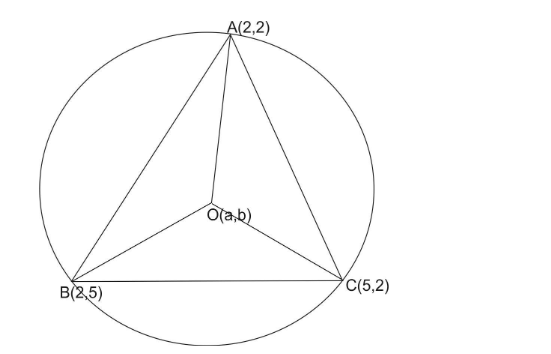
Then,
OA = OB
 $
  \sqrt {{{\left( {a - 2} \right)}^2} + {{\left( {b - 2} \right)}^2}} = \sqrt {{{\left( {a - 2} \right)}^2} + {{\left( {b - 5} \right)}^2}} \\
  Sqauring\,\,both\,\,side\,\,to\,\,remove\,\,square\,\,root. \\
   \Rightarrow {\left( {a - 2} \right)^2} + {\left( {b - 2} \right)^2} = {\left( {a - 2} \right)^2} + {\left( {b - 5} \right)^2} \\
   \Rightarrow {\left( {b - 2} \right)^2} = {\left( {b - 5} \right)^2} \\
   \Rightarrow b - 2 = \pm \left( {b - 5} \right) \\
   \Rightarrow b - 2 = b - 5\,\,\,\,or\,\,\,\,b - 2 = - b + 5 \\
   \Rightarrow 2b = 7 \\
   \Rightarrow b = 3.5 \;
  $
Also, OB = OC
\[
  \sqrt {{{\left( {a - 2} \right)}^2} + {{\left( {b - 5} \right)}^2}} = \sqrt {{{\left( {a - 5} \right)}^2} + {{\left( {b - 2} \right)}^2}} \\
  sqauring\,\,both\,\,side\,\, \\
  {\left( {a - 2} \right)^2} + {\left( {b - 5} \right)^2} = {\left( {a - 5} \right)^2} + {\left( {b - 2} \right)^2} \\
 \]
\[
   \Rightarrow {a^2} + 4 - 4a + {b^2} + 25 - 10b = {a^2} + 25 - 10a + {b^2} + 4 - 4b \\
   \Rightarrow {{{a^2}}} + {4} - 4a + {{{b^2}}} + {{25}} - 10b - {{{a^2}}} - {{25}} + 10a - {{{b^2}}} - {4} + 4b = 0 \\
   \Rightarrow 6a - 6b = 0 \\
   \Rightarrow a = b \;
 \]
Substituting value of b from above. We have,
 $ a = 3.5 $
Hence, from above we see that circumcentre of a triangle is $ \left( {3.5,3.5} \right) $
So, the correct answer is “Option C”.

Note: Circumcentre and Incentre are two different terms as students many times confused with them. Circum-centrre is a centre of the circle formed by side bisectors of a given triangle and in-centre is formed from the angle bisector of the angles of a given triangle.