Question

A 2 V battery, a 15 ohm resistor and a potentiometer of 100 cm length, all are connected in series. If the resistance of potentiometer wire is 5 ohm, the potential gradient of the potentiometer wire will be:
A. 0.005 V/cm
B. 0.05 V/cm
C. 0.02 V/cm
D. 0.2 V/cm

Answer 1

Hint: Express the current in the given circuit. The current in the series circuit does not change. Therefore, the current in the wire of the potentiometer is the same as the current in the external resistance. Calculate the potential across the length of the potentiometer wire and use the formula for potential gradient of the wire of length L.

Formula used:
Ohm’s law, \[i = \dfrac{E}{R}\]
Here, E is the emf provided by the battery and R is the total resistance of the circuit.
Potential gradient, \[K = \dfrac{V}{L}\]
Here, \[V\] is the potential across the potentiometer wire and L is the length of the wire.

Complete step by step answer:
We have given that the 2 V battery, a 15 ohm resistor and a potentiometer of 100 cm length, all are connected in series. We can draw the circuit diagram as follows,

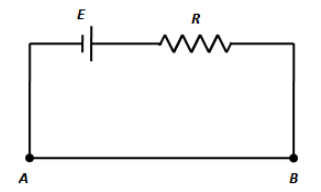
In the above figure, E is the emf of the battery, R is the resistance and AB is the length of the potentiometer wire.Let us determine the current flowing through the above circuit using Ohm’s law as,
\[i = \dfrac{E}{R}\]
Here, E is the emf provided by the battery and R is the total resistance of the circuit.
But, the total resistance in the circuit is the sum of resistance of the circuit and resistance of the potentiometer wire. Therefore, we can write,
\[i = \dfrac{E}{{R + {R_0}}}\]
Here, \[{R_0}\] is the resistance of potentiometer wire.
Substituting \[E = 2\,V\], \[R = 15\,\Omega \] and \[{R_0} = 5\,\Omega \] in the above equation, we get,
\[i = \dfrac{2}{{15 + 5}}\]
\[ \Rightarrow i = 0.1\,{\text{A}}\]

Since the potentiometer wire is in series, the same amount of current will flow through it. We have the formula for the potential gradient of the wire of length L,
\[K = \dfrac{{{V_{AB}}}}{L}\]
Here, \[{V_{AB}}\] is the potential across the potentiometer wire.
The potential across the potentiometer wire can be calculated by using Ohm’s law as follows,
\[{V_{AB}} = i{R_0}\]
\[ \Rightarrow {V_{AB}} = \left( {0.1} \right)\left( 5 \right)\]
\[ \Rightarrow {V_{AB}} = 0.5\,V\]
Now, we can calculate the potential gradient of the wire as follows,
\[K = \dfrac{{{V_{AB}}}}{L}\]
Substituting \[{V_{AB}} = 0.5\,V\] and \[L = 100\,{\text{cm}}\] in the above equation, we get,
\[K = \dfrac{{0.5}}{{100}}\]
\[ \therefore K = 0.005\,{\text{V/cm}}\]

So, the correct answer is option A.

Note:The current in the above circuit is expressed using Kirchhoff’s voltage law. Students must know that the current remains constant in the series circuit even if it encounters a resistance in its path and the voltage does not remain constant in the series as it drops across each component. Note that we are asked to determine the potential gradient in units of V/cm. Therefore, do not convert the length of the wire into meters.