
A 2 MeV proton is moving perpendicular to a uniform magnetic field of 2.5 tesla.
The force on the proton is
(A) $9.6 \times {10^{15}}N$
(B) $7.6 \times {10^{ - 12}}N$
(C) $9.6 \times {10^{12}}N$
(D) $7.6 \times {10^{12}}N$
Answer
581.4k+ views
Hint: To calculate the force on any moving charge particle we use following formula
$\vec F = q(\vec V \times \vec B)$
Where q $ = $ Charge of particle
V $ = $ Velocity of particle
B $ = $ Magnetic field
$\boxed{F = qVB\sin \theta }$
Here $\theta $ is the angle between V & B
Complete step by step solution:
For calculating the magnetic force on protons first we have to analyze motion of the proton with respect to direction of magnetic field.
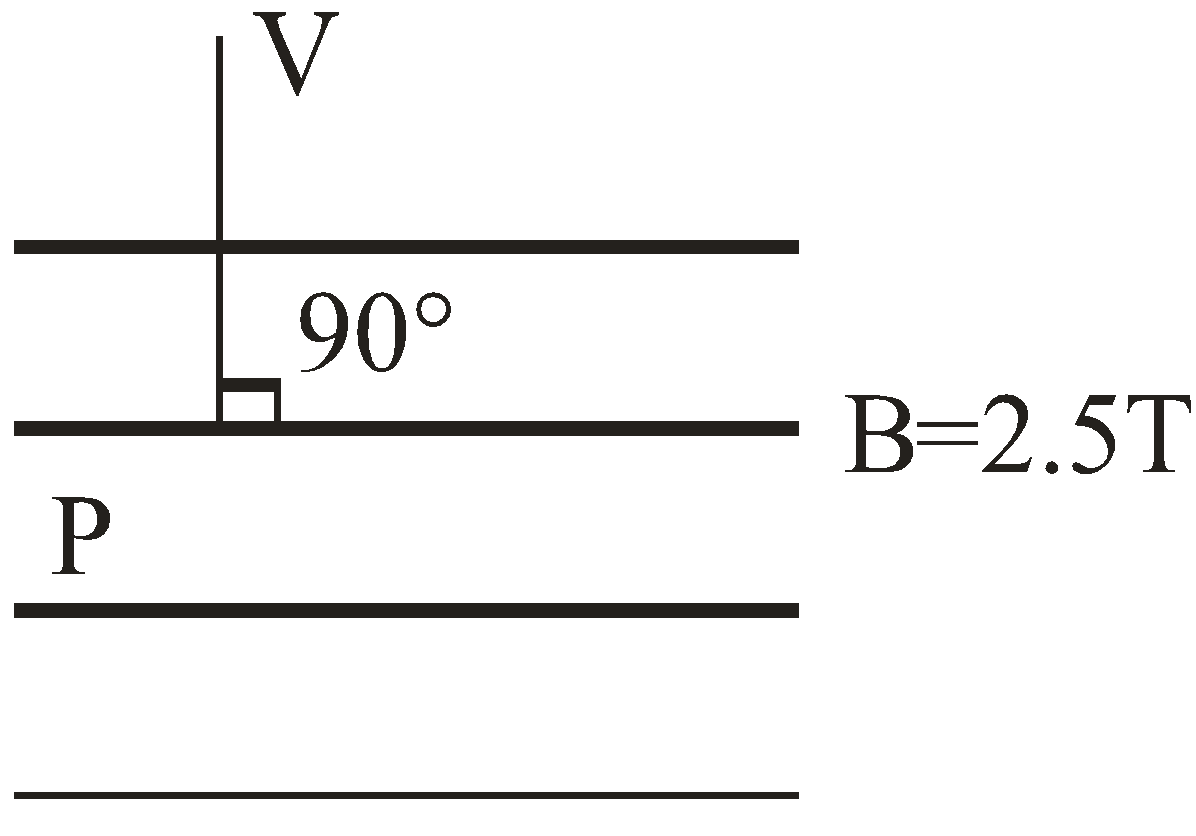
Here given that kinetic charge of proton is 2 MeV
i.e., $K.E = \dfrac{1}{2}m{V^2}$
$\dfrac{1}{2}m{V^2} = 2MeV = 2 \times {10^6} \times 1.6 \times {10^{ - 19}}$
Here m $ = $ mass of proton $ = 1.67 \times {10^{ - 27}}kg$
${V^2} = \dfrac{{2 \times 2 \times {{10}^6} \times 1.6 \times {{10}^{ - 19}}}}{{1.67 \times {{10}^{ - 27}}}}$
${V^2} = \dfrac{{4 \times {{10}^{ - 13}} \times {{10}^{27}} \times 1.6}}{{1.67}}$
${V^2} = 3.832 \times {10^{14}}$
$\boxed{V = 1.957 \times {{10}^7}m/s}$
We know that $\vec F = q(\vec V \times \vec B)$
$F = qVB\sin \theta $
Given that angle between V & B is $90^\circ $
So, $F = qVB\sin 90^\circ $
$F = qVB$
Given $q = 1.6 \times {10^{ - 19}}C,B = 2.5T$
$F = 1.6 \times {10^{ - 19}} \times 1.957 \times {10^7} \times 2.5$
$F \simeq 7.83 \times {10^{ - 12}}N$
So, option B is correct answer.
Note: In order to solve this type of problems first we have to convert the kinetic charge from MeV.
Where $1MeV = 1 \times {10^6} \times 1.6 \times {10^{ - 19}}J$
$\vec F = q(\vec V \times \vec B)$
Where q $ = $ Charge of particle
V $ = $ Velocity of particle
B $ = $ Magnetic field
$\boxed{F = qVB\sin \theta }$
Here $\theta $ is the angle between V & B
Complete step by step solution:
For calculating the magnetic force on protons first we have to analyze motion of the proton with respect to direction of magnetic field.
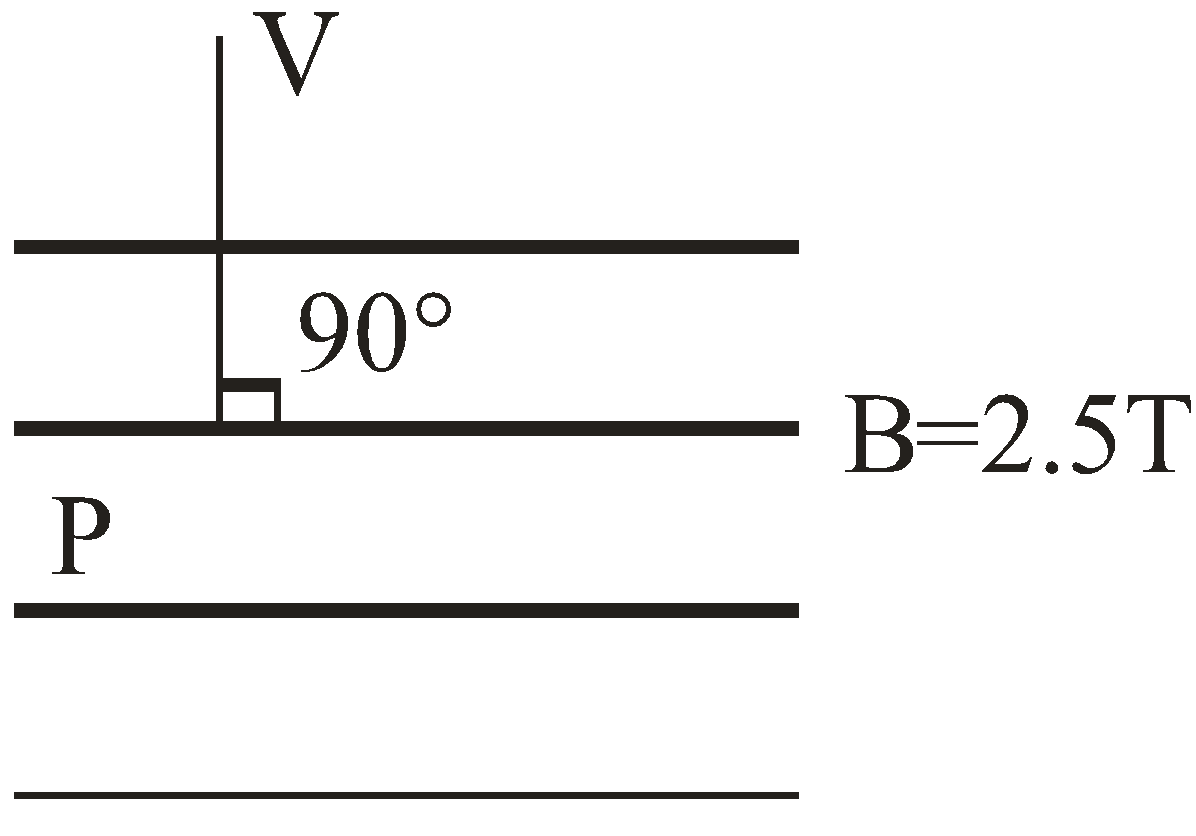
Here given that kinetic charge of proton is 2 MeV
i.e., $K.E = \dfrac{1}{2}m{V^2}$
$\dfrac{1}{2}m{V^2} = 2MeV = 2 \times {10^6} \times 1.6 \times {10^{ - 19}}$
Here m $ = $ mass of proton $ = 1.67 \times {10^{ - 27}}kg$
${V^2} = \dfrac{{2 \times 2 \times {{10}^6} \times 1.6 \times {{10}^{ - 19}}}}{{1.67 \times {{10}^{ - 27}}}}$
${V^2} = \dfrac{{4 \times {{10}^{ - 13}} \times {{10}^{27}} \times 1.6}}{{1.67}}$
${V^2} = 3.832 \times {10^{14}}$
$\boxed{V = 1.957 \times {{10}^7}m/s}$
We know that $\vec F = q(\vec V \times \vec B)$
$F = qVB\sin \theta $
Given that angle between V & B is $90^\circ $
So, $F = qVB\sin 90^\circ $
$F = qVB$
Given $q = 1.6 \times {10^{ - 19}}C,B = 2.5T$
$F = 1.6 \times {10^{ - 19}} \times 1.957 \times {10^7} \times 2.5$
$F \simeq 7.83 \times {10^{ - 12}}N$
So, option B is correct answer.
Note: In order to solve this type of problems first we have to convert the kinetic charge from MeV.
Where $1MeV = 1 \times {10^6} \times 1.6 \times {10^{ - 19}}J$
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
What are the major means of transport Explain each class 12 social science CBSE

Which are the Top 10 Largest Countries of the World?

Draw a labelled sketch of the human eye class 12 physics CBSE

Explain sex determination in humans with line diag class 12 biology CBSE

The pH of the pancreatic juice is A 64 B 86 C 120 D class 12 biology CBSE

Explain sex determination in humans with the help of class 12 biology CBSE




