Question

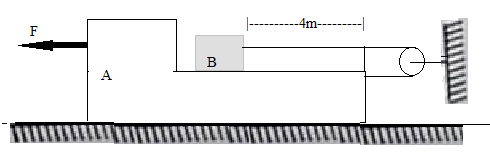
A 1kg block ‘B’ rests as shown on a frictionless bracket ‘A’ of same mass. Consider force \[F = 2N\] starts to act at time \[t = 0\], when the distance of block B from the end of bracket is \[4m\]. Find time (in sec), when block B falls off the bracket.

Answer 1

Hint: In this question Newton’s second Law of motion is used to obtain the acceleration that occurs. After getting the value of acceleration we obtain the value of time t by using the equation of motion. When some forces acting upon an object, then objects have motion in response to those forces.
Newton’s laws of motion are physical laws that are related to mechanics. These laws explain the motion of objects that have a relation between motion and force acting upon it.
The second law states that the force acting upon an object is equal to the product of mass of object and acceleration of the object. In other words the acceleration of an object is directly proportional to the net force acting on it.
If mass of object= \[m\], acceleration of the object= \[a\]
According to Newton’s second law of motion, net force acting upon an object is given by, \[{F_{net}} = m \times a\]

Complete step by step answer:
Given that: \[F = 2N\], \[m = 1kg\], distance of block from end of bracket ,\[s = 4m\], at \[t = 0\],\[u = 0\]
From the above diagram, Resultant force =\[{F_{net}} = F\]
From second law of motion,\[{F_{net}} = m \times a\]
\[{F_{net}} = F = m \times a\]
\[ \Rightarrow m \times a = F\]
\[ \Rightarrow a = \dfrac{F}{m} = \dfrac{2}{1} = 2m{s^{ - 1}}\]
from, equation of motion: \[s = ut + \dfrac{1}{2}a{t^2}\]
\[4 = 0 \times t + \dfrac{1}{2} \times 2 \times {t^2}\]
\[ \Rightarrow 4 = {t^2}\]
\[ \Rightarrow t = 2\sec \]

Hence, the required time is \[2\sec \], when block B falls off the bracket.

Note:
In this question the frictionless bracket is given, so we are not using the formula for friction force. The net force is zero because; only \[2N\] force is working on block B.
In case of 2 forces applied on block B: The net force will be \[{F_{net}} = {F_1} - {F_2}\] (if \[{F_1} > {F_2}\]) or \[{F_{net}} = {F_2} - {F_1}\] if \[{F_2} > {F_1}\], where, \[{F_1}\] and \[{F_2}\] are two forces applied on block in opposite direction.
Here, only 2N force is applied on block B. Students always make mistakes about taking value of net force.