Question

A 14 m wide athletic track consists of two straight sections each 120m long joined by semi-circular ends with an inner radius of 35m. calculate the area of the track.

Answer 1

Hint: This is a problem related to the surface area of 2 D figures mainly rectangle and semi-circle. A rectangle is a 2D shape in geometry, having 4 sides and 4 corners. Its two sides meet at right angles. The opposite sides of a rectangle have the same lengths and are parallel. A semicircle is a 2D figure which is half of a circle
Area of a rectangle= (length ×breadth),
Area of a semi-circle=$\dfrac{1}{2}\pi {r^2}$ .

Complete step by step solution:

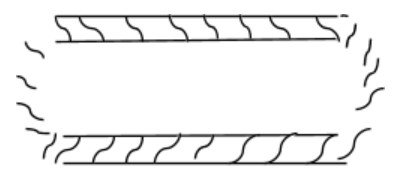
Here we have given a long path of length (l)120 m, which is having semi-circular ends with inner radius 35 m.
Width of track (t)= 14 m
Hence, it can be said that outer radius = 14+35=49 m
Let, R (outer radius) = 49 m
And, r (inner radius) = 35 m.
Therefore, area of the track = area of the shaded region
                        = i.e. area of (two long straight rectangular paths and two semicircular paths)
                     \[\begin{gathered}
   = \,2 \times \left( {120 \times 14} \right) + \,\,2 \times \left( {\dfrac{1}{2}\pi {R^2} - \dfrac{1}{2}\pi {r^2}} \right) \\
   = \,2 \times \left( {1680} \right) + 2\, \times \left( {\dfrac{1}{2}\pi \times \,{{49}^2} - \dfrac{1}{2}\pi \times {{35}^2}} \right) \\
   = \,3360\, + \,2\, \times \dfrac{1}{2}\pi \left( {49 + 35} \right) \times \left( {49 - 35} \right) \\
   = \,3360\,\, + \,\dfrac{{22}}{7} \times 84\, \times 14 \\
   = \,7056\,\,{m^2} \\
\end{gathered} \]

Finally, we got the answer i.e. the area of the athletic track or the area of the shaded region as shown in the figure as, 7056 square meters.

Note: Here we have used the value of π as $\dfrac{{22}}{7}$.
And,${a^2} - {b^2} = (a - b)(a + b)$
These should be carefully kept in mind.