Question

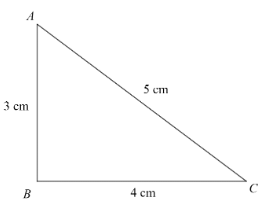
A $ 12\;cm $ wire is given a shape of a right angled triangle $ \;ABC $ having sides $ 3\;cm $ , $ 4\;cm $ , and $ 5\;cm $ as shown in the figure. The resistance between two ends $ (AB,BC,CA) $ of the respective sides are measured one by one by a multimeter. The resistances will be in the ratio?

(A) $ \;3:4:5 $
(B) $ \;9:16:25 $
(C) $ \;27:32:35 $
(D) $ \;21:24:25 $

Answer 1

Hint: To find the ratio of resistances between two ends, we need to rearrange the connection as per the considered ends, and find the equivalent resistances separately and then find the ratio of all resistances.

Complete answer:
From the given data,
Length of the component $ A\;B $ , $ {{l}_{1}}=3cm $
Length of the component $ B\;C $ , $ {{l}_{2}}=4cm $
Length of the component $ A\;C $ , $ {{l}_{3}}=5cm $
Now, we know that the resistance can be calculated as,
 $ R = \dfrac{{\rho}l}{A} $
Where $ \rho $ is the resistivity of the wire, $ l $ is the length of the wire, $ A $ is the area of the cross section of the wire.
Now, for all three resistances, the resistance is calculated as
 $ {{R}_{1}}=\dfrac{{{\rho }_{1}}{{l}_{1}}}{{{A}_{1}}} $
 $ {{R}_{2}}=\dfrac{{{\rho }_{2}}{{l}_{2}}}{{{A}_{2}}} $
 $ {{R}_{3}}=\dfrac{{{\rho }_{3}}{{l}_{3}}}{{{A}_{3}}} $
But here as per the given conditions, a single uniform wire is bent to make the triangle.
Hence, the resistivity of all three components and the area of the cross section of all three components are the same.
 $ \therefore \dfrac{{{\rho }_{1}}}{{{A}_{1}}}=\dfrac{{{\rho }_{2}}}{{{A}_{2}}}=\dfrac{{{\rho }_{3}}}{{{A}_{3}}} $
Suppose all the ratios as a single variable
 $ \therefore \dfrac{{{\rho }_{1}}}{{{A}_{1}}}=\dfrac{{{\rho }_{2}}}{{{A}_{2}}}=\dfrac{{{\rho }_{3}}}{{{A}_{3}}}=a(suppose) $
Now, the values of all three resistances by substituting the given values of lengths is
 $ {{R}_{1}}=3a\Omega $ , $ {{R}_{2}}=4a\Omega $ , $ {{R}_{3}}=5a\Omega $
Now, for simplicity of calculation we will not consider the variable
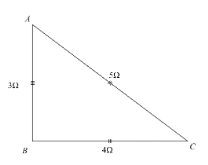
 $ {{R}_{1}}=3\Omega $ , $ {{R}_{2}}=4\Omega $ , $ {{R}_{3}}=5\Omega $
Hence, the figure can be shown as
 

Now, we will consider the individual components of the connection
Resistance across the ends $ A $ and $ B $
For the considered ends, the circuit can be explained as $ R_2 $ and $ R_3 $ connected in series connection and whole connected in parallel connection with $ R_1 $ as shown below,

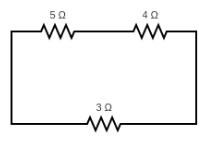
Equivalent resistance for the resistors $ R_2 $ and $ R_3 $ is
 $ R'={{R}_{2}}+{{R}_{3}} $
Substituting the values,
 $ R'=4\Omega +5\Omega $
 $ \therefore R'=9\Omega $
This equivalent resistance and $ R_1 $ are connected in parallel. Hence, the equivalent resistance is
 $ {{R}_{eq}}=\dfrac{{{R}_{1}}R'}{{{R}_{1}}+R'} $
Substituting the values,
 $ \therefore {{R}_{eq1}}=\dfrac{3\times 9}{3+9} $
 $ \therefore {{R}_{eq1}}=\dfrac{27}{12}\Omega $ …… $ (1) $
Resistance across the ends $ B $ and $ C $
For the considered ends, the circuit can be explained as $ R_1 $ and $ R_3 $ connected in series connection and whole connected in parallel connection with $ R_2 $ as shown below,

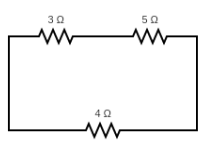
Equivalent resistance for the resistors $ R_1 $ and $ R_3 $ is
 $ R'={{R}_{1}}+{{R}_{3}} $
Substituting the values,
 $ R'=3\Omega +5\Omega $
 $ \therefore R'=8\Omega $
This equivalent resistance and $ R_2 $ are connected in parallel. Hence, the equivalent resistance is
 $ {{R}_{eq}}=\dfrac{{{R}_{2}}R'}{{{R}_{2}}+R'} $
Substituting the values,
 $ \therefore {{R}_{eq2}}=\dfrac{4\times 8}{4+8} $
 $ \therefore {{R}_{eq2}}=\dfrac{32}{12}\Omega $ …… $ (2) $
Resistance across the ends $ C $ and $ A $
For the considered ends, the circuit can be explained as $ R_1 $ and $ R_2 $ connected in series connection and whole connected in parallel connection with $ R_3 $ as shown below,

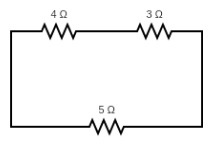
Equivalent resistance for the resistors $ R_1 $ and $ R_2 $ is
 $ R'={{R}_{1}}+{{R}_{2}} $
Substituting the values,
 $ R'=3\Omega +4\Omega $
 $ \therefore R'=7\Omega $
This equivalent resistance and $ R_3 $ are connected in parallel. Hence, the equivalent resistance is
 $ {{R}_{eq}}=\dfrac{{{R}_{3}}R'}{{{R}_{3}}+R'} $
Substituting the values,
 $ \therefore {{R}_{eq3}}=\dfrac{5\times 7}{5+7} $
 $ \therefore {{R}_{eq3}}=\dfrac{35}{12}\Omega $ …… $ (3) $
Taking the ratio of all the cases,
 $ {{R}_{eq1}}:{{R}_{eq2}}:{{R}_{eq3}}=\dfrac{27}{12}:\dfrac{32}{12}:\dfrac{35}{12} $
 $ \therefore {{R}_{eq1}}:{{R}_{eq2}}:{{R}_{eq3}}=27:32:35 $
Hence, the correct answer is Option $ (C) $ .

Note:
The value of the resistances are directly taken equal to the length of the resistances for simplicity, as they are considered in a ratio and the common factor will be canceled eventually. However, this can only be done, if all the three wires are given to be of the same material and same area.