Question

A 10m long horizontal wire extends from North East to South West. It is falling with a speed of $5.0m{s^{ - 1}},$ at right angles to the horizontal component of the earth’s magnetic field, of $0.3 \times {10^{ - 4}}{\text{Wb/}}{{\text{m}}^2}$. The value of the induced emf in wire is:
(A) $2.5 \times {10^{ - 3}}{\text{V}}$
(B) $1.1 \times {10^{ - 3}}{\text{V}}$
(C) $0.3 \times {10^{ - 3}}{\text{V}}$
(D) $1.5 \times {10^{ - 3}}{\text{V}}$

Answer 1

Hint:
To solve this question, we need to use the formula for the motional emf induced. We have to analyse the situation of the conductor, and write each of the variables in terms of the vector representation. Then, substituting these vectors in the emf equation will give the required emf induced in the rod.
Formula used: The formula used to solve this question is
$e = \left( {\vec v \times \vec B} \right) \cdot \vec l$
Where $e$ is the emf induced in a conductor $\vec v$ is the velocity of the conductor, $\vec B$ is the magnetic field, and $\vec l$ is the length of the rod.

Complete step by step answer:
The situation is shown in the below diagram.

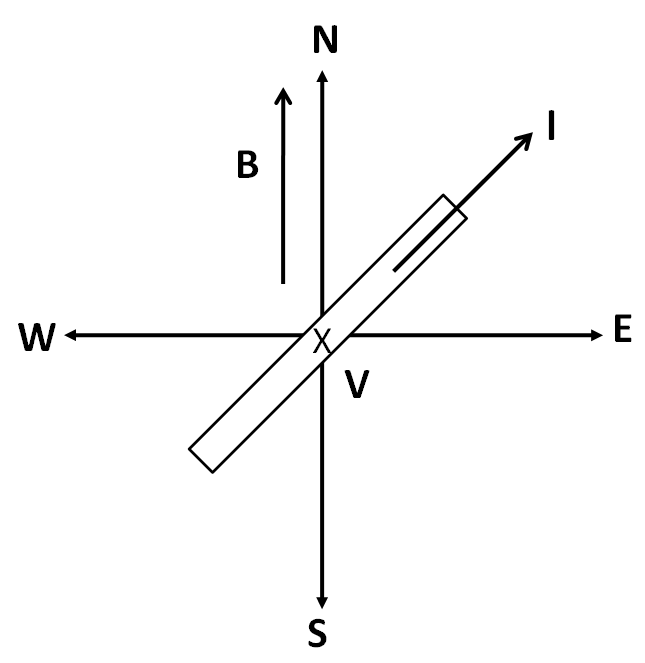
We know that the emf induced in a conductor due to its motion in a magnetic field is given by
$e = \left( {\vec v \times \vec B} \right) \cdot \vec l$
According to the question, $\vec v = - 5.0\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k} {\text{ }}m/s$\[\vec B = 0.3 \times {10^{ - 4}}{\text{ }}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{j} Wb/{m^2}\], and $\vec l = 10\left( {\frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{i} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{j} }}{{\sqrt 2 }}} \right)m$
(the directions of each of the vectors are shown in the figure)
Substituting these in the emf equation, we get
\[e = ( - 5.0\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k} \times 0.3 \times {10^{ - 4}}{\text{ }}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{j} ) \cdot \frac{{10}}{{\sqrt 2 }}\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{i} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{j} } \right)\]
We know that \[\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k} \times {\text{ }}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{j} = - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{i} \]
\[\therefore e = 1.5 \times {10^{ - 4}} \times \frac{{10}}{{\sqrt 2 }}i \cdot \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{i} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{j} } \right)\]
$e = 1.1 \times {10^{ - 3}}{\text{V}}$
Therefore, the emf induced in the rod is equal to $1.1 \times {10^{ - 3}}{\text{V}}$.

Note:
It is always preferred to write the emf equation in terms of the vectors, as there is a high chance of committing mistakes in calculating the emf. Only the components of the length, the velocity of the conductor and the magnetic field, which are mutually perpendicular are multiplied together to get the emf induced.