Question

A $10{\text{g}}$ bullet moving directly upward at $1000{\text{m}}{{\text{s}}^{ - 1}}$ strikes and passes through the centre of mass of a $10{\text{kg}}$ block, initially at rest. The bullet emerges from the block moving directly upward at $400{\text{m}}{{\text{s}}^{ - 1}}$ . Find the velocity of the block just after the bullet comes out of it.

A) $1{\text{m}}{{\text{s}}^{ - 1}}$
B) ${\text{0}} \cdot {\text{4m}}{{\text{s}}^{ - 1}}$
C) $1 \cdot 4{\text{m}}{{\text{s}}^{ - 1}}$
D) ${\text{0}} \cdot {\text{6m}}{{\text{s}}^{ - 1}}$

Answer 1

Hint:Here the bullet can be viewed to collide with a block of mass at rest. Immediately after the collision, the block of mass will move for a short distance as the bullet comes out of it. Though gravity acts during the collision, its impulse is negligible. We can employ the conservation of linear momentum principle to determine the velocity of the block.

Formula used:
-The linear momentum of a body is given by, $p = mv$ where $m$ is the mass of the body and $v$ is its velocity.

Complete step by step solution.
Step 1: Sketch a figure depicting the system before and after the collision and list the key details involved.

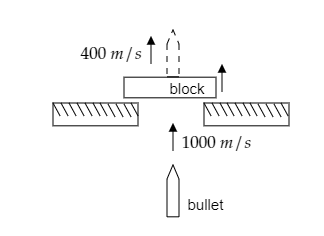
The mass of the bullet is given to be $m = 10{\text{g}}$ and its velocity before striking is given to be ${u_1} = 1000{\text{m}}{{\text{s}}^{ - 1}}$ .
The mass of the block is given to be $M = 10{\text{kg}}$ .
Since it is mentioned to be at rest, its velocity before striking will be ${u_2} = 0{\text{m}}{{\text{s}}^{ - 1}}$ .
The velocity of the bullet after striking the block is given to be ${v_1} = 400{\text{m}}{{\text{s}}^{ - 1}}$ .
Let ${v_2}$ be the velocity of the block immediately after the bullet comes out of it which is to be determined.
Step 2: Apply the conservation of momentum principle to obtain the value of ${v_2}$ .
In any collision, the total momentum of the system before and after the collision will be the same.
i.e., ${p_{before}} = {p_{after}}$ --------- (1)
The momentum of the system before the collision is expressed as ${p_{before}} = m{u_1} + M{u_2}$ ------- (2)
The momentum of the system after the collision is expressed as ${p_{after}} = m{v_1} + M{v_2}$ ------- (3)
Substituting equations (2) and (3) in equation (1) we get, $m{u_1} + M{u_2} = m{v_1} + M{v_2}$

$ \Rightarrow {v_2} = \dfrac{{m{u_1} + M{u_2} - m{v_1}}}{M}$ -------- (4)

Substituting for $m = 0 \cdot 01{\text{kg}}$ , $M = 10{\text{kg}}$ , ${u_1} = 1000{\text{m}}{{\text{s}}^{ - 1}}$ and ${u_2} = 0{\text{m}}{{\text{s}}^{ - 1}}$ in equation (4) we get, ${v_2} = \dfrac{{\left( {0 \cdot 01 \times 1000} \right) + \left( {10 \times 0} \right) - \left( {0 \cdot 01 \times 400} \right)}}{{10}} = 0 \cdot 6{\text{m}}{{\text{s}}^{ - 1}}$
$\therefore $ the velocity of the block just as the bullet comes out of it is obtained to be ${v_2} = 0 \cdot 6{\text{m}}{{\text{s}}^{ - 1}}$ .

So the correct option is D.

Note:Here the system comprises the bullet and block of mass. When substituting values of the different physical quantities in an equation, make sure that all the quantities are expressed in their respective S.I units. If not, then the necessary conversion of units must be employed. Here the mass of the bullet was given in the unit of gram, so we converted it into the S.I unit of kilogram as $m = 10{\text{g}} = 10 \times {10^{ - 3}}{\text{kg}} = 0 \cdot 01{\text{kg}}$ before substituting in equation (4).