Question

A 10cm long rod AB moves with its ends on two mutually perpendicular straight lines OX and OY. If the end $A$ be moving at the rate of $2$ $\dfrac{{cm}}{s}$,then when the distance of $A$ from $O$ is $8\,cm$, the rate at which the end $B$ is moving, is
1. $\dfrac{8}{3}$ $\dfrac{{cm}}{s}$
2. $\dfrac{4}{3}$ $\dfrac{{cm}}{s}$
3. $\dfrac{2}{9}$ $\dfrac{{cm}}{s}$
4. None of these

Answer 1

Hint: Here we use the concept of rate of change of quantities.
 If a quantity $y$ varies with another quantity $x$, then $\dfrac{{dy}}{{dx}}$ represents the rate of change of $y$ with respect to $x$ .
Here it is given that rod AB moves with its ends on two mutually perpendicular straight lines OX and OY. Let the end $A$ of rod move on line OX with respect to time $t$ and end $B$ of rod move on line OY with respect to time $t$ .
Let the distance from point $A$ to point $O$ be $x$ and the distance from point $B$ to point $O$ be $y$
This can be represented by following diagram

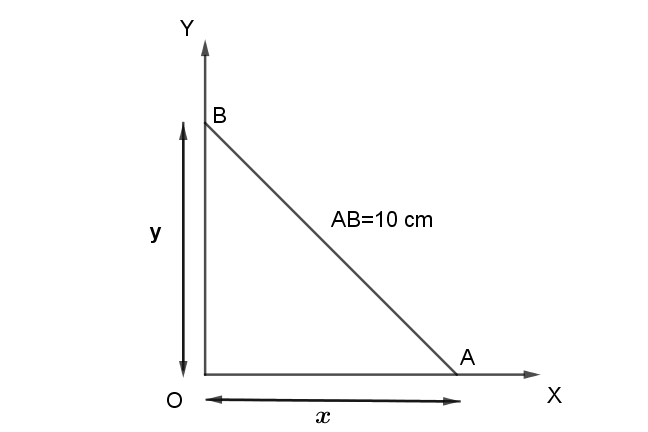
We are asked to find the rate at which the end $B$ is moving i,e $\dfrac{{dy}}{{dt}}$

Complete step-by-step solution:
From the figure, we know that $\Delta BOA$ is a right angled triangle.
Therefore, from Pythagoras theorem we get,
${x^2} + {y^2} = {10^2} ----------- \left( 1 \right)$
Differentiating the above equation with respect to time $t$ , we get
$2x\dfrac{{dx}}{{dt}} + 2y\dfrac{{dy}}{{dt}} = 0 ------ \left( 2 \right)$
It is given that end $A$ is moving at the rate of $2$ $\dfrac{{cm}}{s}$ i,e $\dfrac{{dx}}{{dt}} = 2$ $\dfrac{{cm}}{s}$
and the distance of $A$ from $O$ is $8$$cm$ i,e $x = 8$$cm$
Substituting the value of $x$ in equation $\left( 1 \right)$ , we get
${8^2} + {y^2} = {10^2}$
$ \Rightarrow {y^2} = 100 - 64$
$ \Rightarrow y = \sqrt {36} $
$y = 6$ $cm$
Hence the distance from point $B$ to point $O$ is $6\,cm$.
Now substituting the values in equation $\left( 2 \right)$ , we get
$2 \times 8 \times 2 + 2 \times 6 \times \dfrac{{dy}}{{dt}} = 0$
On simplifying we get,
$12\dfrac{{dy}}{{dt}} = - 32$
$ \Rightarrow \dfrac{{dy}}{{dt}} = \dfrac{{ - 32}}{{12}}$
On cancelling numerator and denominator by 4 , we get
$\dfrac{{dy}}{{dt}} = \dfrac{{ - 8}}{3}$ $\dfrac{{cm}}{s}$
$\therefore \dfrac{{dy}}{{dt}} = \dfrac{8}{3}$ $\dfrac{{cm}}{s}$
The rate at which the end $B$ is moving is $\dfrac{8}{3}$ $\dfrac{{cm}}{s}$ .

Note: It is very important to note that the derivative of a constant is zero.
Many students go wrong here.
In the above equation
${x^2} + {y^2} = {10^2}$
On differentiating the above equation we get
$2x\dfrac{{dx}}{{dt}} + 2y\dfrac{{dy}}{{dt}} = 0$
Not $2x\dfrac{{dx}}{{dt}} + 2y\dfrac{{dy}}{{dt}} = 100$
Also derivative of ${x^2}$ with respect to time $t$ is $2x\dfrac{{dx}}{{dt}}$ as $x$ varies with time $t$ .