Question

A $100$m train is moving North at a speed of $16\;m{s^{ - 1}}$. A bird flying at $4\;m{s^{ - 1}}$towards South crosses the train in
A. $5s$
B. $10s$
C. $12s$
D. $20s$

Answer 1

Hint: In such questions, calculate the relative velocity then use equation V = D/T

Complete step by step solution:
It is given that two objects are moving in opposite directions so we need to find the relative velocity of one with respect to another.
Take direction of velocity in direction of bird movement (South) as positive.

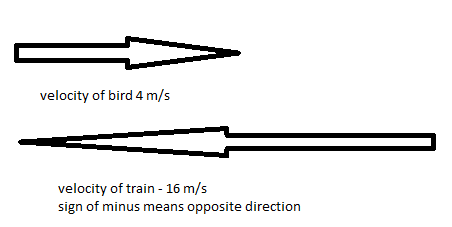
Velocity of bird, \[{v_{bird}} = 4m/s\]
As train movement is in opposite direction (North), so minus sign will be applied
Velocity of train, \[{v_{train}} = - 16m/s\]
Relative velocity of bird w.r.t train, \[{v_{birdtrain}} = 4 - \left( { - 16} \right) = 20m/s\]
\[Time{\text{ }} = {\text{ }}\dfrac{{Distance}}{{Velocity}}\]
The distance to be covered by bird is the length of the train as per our question
Time$ = $length of train/relative velocity of bird
\[T = \dfrac{{100}}{{20}}{\text{ }} = 5sec\]

Hence, time to cover train length is 5sec.

So the correct option is (A), $5$ sec.

Note: Sometimes velocity of train is given in terms of Km/hr then you have to convert it to m/s by using the conversion \[\dfrac{{1000}}{{3600}}{\text{ }} = {\text{ }}\dfrac{5}{{18}}\]. If a train has a speed of x km/hr then in m/s it will be \[\dfrac{{5x}}{{18}}{\text{ }}m/s\].