Question

A $1000kg$ lift is tied with metallic wires of maximum safe stress of $1.4\times {{10}^{8}}N{{m}^{-2}}$. If the maximum acceleration of the lift is $1.2m\,{{s}^{-2}}$, then the minimum diameter of the wire is-
(A).$0.01m$
(B). $0.01cm$
(C). $0.001m$
(D). $0.02cm$

Answer 1

Hint: As the lift is accelerating there is a net force acting on it. Using Newton’s second law of motion, we can calculate the tension which is the force acting in the wire. The Stress is the force acting per unit area.The Stress acting in a material is inversely proportional to the diameter of the material.

Formulae Used:
$mg-T=ma$
$stress=\dfrac{F}{A}$
$\text{max stress}=\dfrac{T}{\pi {{({{r}_{\min }})}^{2}}}$
$\text{diameter=2 }\!\!\times\!\!\text{ radius}$

Complete step-by-step solution:
The lift is accelerating downwards; therefore, the forces acting on it are-

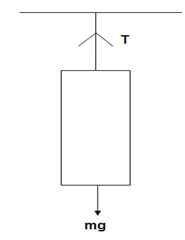
$mg-T=ma$
Given, $a=1.2\times {{10}^{-2}}m{{s}^{-2}},\,m=1000kg$.
Substituting in the above eq, we get
$T=1000(9.8+1.2)$
$\therefore T=1.1\times {{10}^{4}}N$-------- (1)
Stress is the force acting per unit area. Its SI unit is $N{{m}^{2}}$. It is given by-
$stress=\dfrac{F}{A}$
Here,
$F$ is the force
$A$ is the area of cross section
For maximum stress, the diameter must be minimum-
$\text{max stress}=\dfrac{T}{\pi {{({{r}_{\min }})}^{2}}}$
$\begin{align}
  & \Rightarrow 1.4\times {{10}^{8}}=\dfrac{1.1\times {{10}^{4}}}{\pi {{({{r}_{\min }})}^{2}}} \\
 & \Rightarrow {{r}_{\min }}^{2}=25\times {{10}^{-6}} \\
\end{align}$
$\therefore {{r}_{\min }}=5\times {{10}^{-3}}m$
We know that $\text{diameter=2 }\!\!\times\!\!\text{ radius}$
$\Rightarrow {{d}_{\min }}=2\times {{r}_{\min }}$
$\therefore {{d}_{\min }}=0.01m$

The minimum diameter of a wire that can be used to support the lift is $0.01m$.

Hence, the correct option is (A).

Additional Information:
Tensile strength is defined as the maximum load that a material can support without breaking divided by the area of cross-section of the material. Its SI unit is $N\,{{m}^{-2}}$. An object experiences some deformations when a stress is applied, when the stress is less than the tensile strength, the object returns to its original shape.

Note:
Tension is the pulling force present in a string, rod, or another similar one-dimensional lifting object. The tension in the string is due to the gravitational force acting on the lift. There is net force acting on the lift. So by Newton's second law of motion, it undergoes acceleration.