Question

A 10 D lens is used as a magnifier. The distance where the object should be placed to obtain maximum angular magnification for a normal eye (near point 25 cm) is

Answer 1

Hint: We are given the power of a lens which is used as a magnifier. We know that when we obtain maximum angular magnification, the image will be formed at the near point of the eye. By obtaining focal length from power and substituting the known values in the lens formula, we will get the solution.
Formula used:
Power of a lens, $P=\dfrac{1}{f}$
Lens formula, $\dfrac{1}{f}=\dfrac{1}{v}-\dfrac{1}{u}$

Complete answer:
In the question we are given the power of a lens and it is said the lens is used as a magnifier.
We know that when we obtain maximum angular magnification, the image will be formed at the near point of eye.
Here the near point is given as 25 cm.
Since the image is formed at near point, we can write that
$v=-25cm$
The power of the lens is given as 10 D, i.e.
$P=10D$
We know that power,
$P=\dfrac{1}{f}$, were ‘f’ is the focal length of the lens.
By substituting the given value of power in the above equation, we get
$\Rightarrow 10=\dfrac{1}{f}$
$\Rightarrow f=\dfrac{1}{10}m$
By converting to centimeter, we get
$\Rightarrow f=\dfrac{100}{10}cm$
$\Rightarrow f=10cm$
Now let us apply the lens formula.
According to lens formula we know that,
$\dfrac{1}{f}=\dfrac{1}{v}-\dfrac{1}{u}$, were ‘f’ is the focal length, ‘v’ is the image distance and ‘u’ is the object distance.
From earlier calculations we know the value of focal length and image distance. By substituting them in the lens formula, we get
$\Rightarrow \dfrac{1}{10}=\dfrac{1}{-25}-\dfrac{1}{u}$
$\Rightarrow \dfrac{1}{10}+\dfrac{1}{25}=-\dfrac{1}{u}$
From the above equation, we can solve for ‘u’.
$\Rightarrow -\dfrac{1}{u}=\dfrac{35}{250}=\dfrac{7}{50}$
$\Rightarrow \dfrac{1}{u}=-\dfrac{7}{50}$
$\Rightarrow u=-\dfrac{50}{7}$
$\Rightarrow u=-7.14cm$
Hence the object should be kept at –7.14 cm distance to obtain maximum angular magnification for a normal eye.

Note:
Consider the figure of the convex mirror given below.

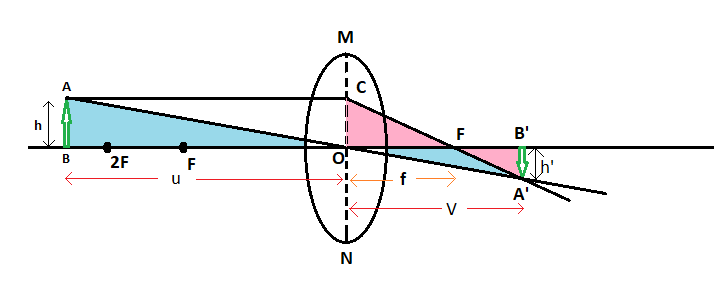
In the figure AB is the object and A’B’ is the image.
‘u’ is the object distance, ‘v’ is the image distance, ‘f’ is the focal length, ‘h’ is the length of the object and ‘h’’ is the length of the image.
Let ‘O’ be the optical centre of the lens, ‘F’ be the principal focus.
Now let us consider the triangle ABO and triangle A’B’O.
We can see that these two triangles are similar.
Therefore,
$\dfrac{A'B'}{AB}=\dfrac{OB'}{OB}$
Similarly we can see that triangle A’B’F and triangle OCF are similar.
Therefore,
$\dfrac{A'B'}{OC}=\dfrac{FB'}{OF}$
But we know that $OC=AB$
Therefore we get,
$\dfrac{A'B'}{AB}=\dfrac{FB'}{OF}$
Now we have,
$\dfrac{A'B'}{AB}=\dfrac{OB'}{OB}\text{ and }\dfrac{A'B'}{AB}=\dfrac{FB'}{OF}$
Since the left hand sides of both these equations are the same, we can equate the right hand side. Thus we get,
$\dfrac{OB'}{OB}=\dfrac{FB'}{OF}$
From the figure we can see that $FB'=OB'-OF$. By substituting this in the above equation, we get
$\dfrac{OB'}{OB}=\dfrac{OB'-OF}{OF}$
We know that
$OB=-u$
$OB'=v$
$OF=f$
Now let us substitute this, thus we get
$-\dfrac{v}{u}=\dfrac{v-f}{f}$
$\Rightarrow vf=-uv+uf$
$\Rightarrow uv=uf-vf$
Now let us divide the whole equation with $uvf$
Therefore,
$\Rightarrow \dfrac{uv}{uvf}=\dfrac{uf}{uvf}-\dfrac{vf}{uvf}$
By simplifying this we get,
$\Rightarrow \dfrac{1}{f}=\dfrac{1}{v}-\dfrac{1}{u}$
This is known as the lens formula.