Question

40 children were asked if they have a computer or a phone or both. The Venn diagram shows the results.

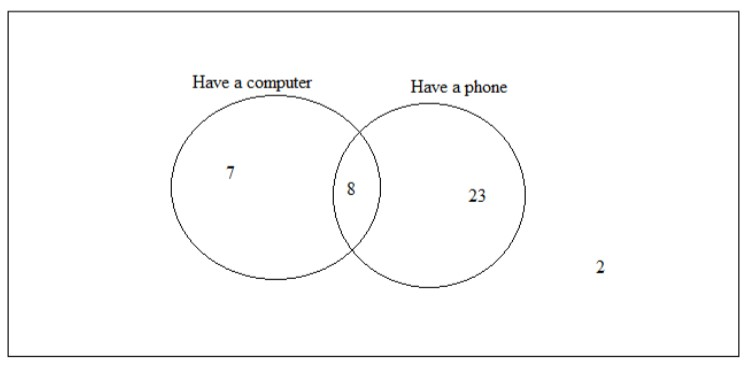
${\rm{i)}}$ A child is chosen at random from the children who have a computer.
Write down the probability that this also has a phone.
${\rm{ii)}}$ Complete the Venn diagram.

Answer 1

Solution i):
Hint: In this problem it is given that 40 children were asked if they have a computer or a phone
or both and a child is chosen at random from the children who have a computer. We have to find
the probability that this also has a phone. Firstly, we numbering the children whose having
computer and phone. Then use the conditional probability and simplify the problem.
It is given that 40 children were asked if they have a computer or a phone or both. And a child is
chosen at random from the children who have a computer we have to find the probability of child
chosen at random from the children who have a computer also has a phone.
Let,
A$ = $ Number of children having computer
B$ = $ Number of children having phones.
C$ = $ Number of children having neither a computer nor a phone.
D$ = $ Number of children. having either a computer and phone or both.
Now, from the figure
$n\left( {\rm{A}} \right) = 5 + 7 = 15$

$n\left( {\rm{B}} \right) = 23 + 8 = 31$
$n\left( {\rm{C}} \right) = 2$
$n\left( {\rm{D}} \right) = 40 - 2 = 38$
$n\left( {{\rm{A}} \cap {\rm{B}}} \right) = 8$
Using conditional probability, we have
$P\left( {\rm{A}} \right) = \dfrac{{n\left( {\rm{A}} \right)}}{{n\left( {\rm{D}} \right)}}$
Substitute $15$ for $n\left( {\rm{A}} \right)$ and 40 for $n\left( {\rm{D}} \right)$ in the above
equation.
$P\left( {\rm{A}} \right) = \dfrac{{15}}{{38}}$
$P\left( {\rm{B}} \right) = \dfrac{{n\left( {\rm{B}} \right)}}{{n\left( {\rm{D}} \right)}}$
Substitute 31 for $n\left( {\rm{B}} \right)$ and 40 for $n\left( {\rm{D}} \right)$ in the above
equation.
$P\left( {\rm{B}} \right) = \dfrac{{31}}{{38}}$
$P\left( {{\rm{A}} \cap {\rm{B}}} \right) = \dfrac{{n\left( {{\rm{A}} \cap {\rm{B}}}
\right)}}{{n\left( {\rm{D}} \right)}}$
Substitute 8 for $n\left( {{\rm{A}} \cap {\rm{B}}} \right)$ and 40 for $n\left( {\rm{D}}
\right)$ in the above equation
$P\left( {{\rm{A}} \cap {\rm{B}}} \right) = \dfrac{8}{{38}}$
Now, the probability of a child being chosen at random from the children who have a phone is.
$\begin{array}{l}P\left( {\dfrac{{\rm{B}}}{{\rm{A}}}} \right) = \dfrac{{P\left( {{\rm{A}}
\cap {\rm{B}}} \right)}}{{P\left( {\rm{A}} \right)}}\\\end{array}$
Substitute $\dfrac{8}{{38}}$ for $P\left( {{\rm{A}} \cap {\rm{B}}} \right)$ and
$\dfrac{{15}}{{38}}$ for $P\left( {\rm{A}} \right)$ in the above expression.
$P\left( {\dfrac{{\rm{B}}}{{\rm{A}}}} \right) =
\dfrac{{\dfrac{8}{{38}}}}{{\dfrac{{15}}{{38}}}} = \dfrac{8}{{15}}$
Thus, the probability of child is chosen at random from the children who have a phone is
$\dfrac{8}{{15}}$

Note: Here, we use a conditional probability formula and simply solve the problem. Then finally
we get the answer.
Solution ${\rm{ii)}}$
Hint: In this problem we have to find the probability of children whose do not have computer
and phone. By the help of the above solution (i) we easily solve the problem.
Let,
X$ = $ Number of children does not have computer
Y$ = $ Number of children does not have phone
Now, we have from the above solution
Probability of children having computer is $P\left( {\rm{A}} \right) = \dfrac{{15}}{{38}}$
And
Probability of children having phone is $P\left( {\rm{B}} \right) = \dfrac{{31}}{{38}}$
To determine the probability of children does not have computer we need to subtract the
probability of children having a computer from 1.
Probability of children does not have computer is
$P\left( {\rm{X}} \right) = 1 - \dfrac{{15}}{{38}} = \dfrac{{23}}{{38}}$
Again, to determine the probability of children does not have phone we need to subtract the
probability of children having a phone from 1.
Probability of children does not have a phone is
$P\left( {\rm{Y}} \right) = 1 - \dfrac{{31}}{{38}} = \dfrac{7}{{38}}$
Note: Here we first consider the number children who do not have computer and phone
respectively.
Then we use the result part of solution (i) and simply solve the problem. Finally, we get our result.