Question

How many 3 letter words can be formed using a, b, c, d, e if
A.repetition of letters is not allowed?
B.repetition of letters allowed?

Answer 1

Hint: In this question, we have to find the number of 3 letter words that can be formed using a, b, c, d, and e. If repetition is allowed then we can take that letter again. So, we have 5 intakes for every three places of 3 letter words.

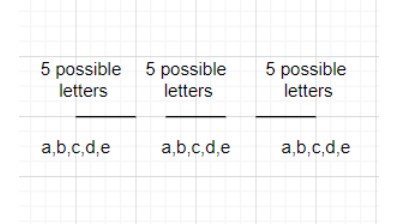
Complete step-by-step answer:
The total number of words \[=5\times 5\times 5=125\] . Now, if repetition is not allowed then we have to take only three letters out of 5 letters. The number of ways to select 3 letters out of 5 letters is \[^{5}{{C}_{3}}\] . But the letter can also be rearranged. The number of ways to rearrange 3 letters are \[3!\] . The total number of 3 letter words is \[^{5}{{C}_{3}}\times 3!\] .
Now, we have to find the number of 3 letter words if repetition is not allowed. That is we have to take 3 letters and we are given 5 letters. The number of 3 letter words that can be formed using 5 letters is \[^{5}{{C}_{3}}\] .
We know that words can be formed after rearranging also. So, the number of rearrangements is \[3!\] .
Now, the total number of words that can be formed \[{{=}^{5}}{{C}_{3}}\times 3!=60\] .
In case (ii), we have to find the number of three-letter words that can be formed if repetition is allowed. As repetition is allowed we can take that letter again if it is taken previously. In the first place, we can take a, b, c, d, and e. So, we have 5 intakes in the first place. Suppose, we take “a” in the first place of 3 letter words. We can also take the letter “a” in the second place too. So, in second place we can take a, b, c, d, and e. In the second place, we have 5 intakes. Similarly, in third place, we have 5 intakes.

The total number of words to be formed \[=5\times 5\times 5=125\] .

Note: In this question, the mistake is generally done in finding the number of words that can be formed without repetition. As we have to take three letters out of five given letters, one can directly write \[^{5}{{C}_{3}}\] . But, the three words can rearrange also. So, we also have to think about the rearrangements.