Question

2 cubes of volume \[64 {\rm{c}}{{\rm{m}}^3}\] are joined end to end. Find the surface area of the resulting cuboid.

Answer 1

Hint: Here, we need to find the surface area of the resulting cuboid. First, we will find the length of the side of the two cubes. Then, we will find the dimensions of the resulting cuboid when the two cubes are joined end to end. We will then use the formula for total surface area of a cuboid and simplify it to find the required answer.

Formula used: We will use the following formula to solve the questions:
The volume of a cube is given by the formula \[V = {a^3}\], where \[a\] is the length of the side of the cube.
The total surface area of a cuboid is given by the formula \[2\left( {lb + bh + lh} \right)\], where \[l\] is the length, \[b\] is the breadth, and \[h\] is the height.

Complete step-by-step answer:
First, we will find the length of the side of the cubes using the formula for volume of a cube.
The volume of a cube is given by the formula \[V = {a^3}\], where \[a\] is the length of the side of the cube.
Substituting \[V = 64{\rm{ c}}{{\rm{m}}^3}\] in the formula, we get
\[ \Rightarrow 64 = {a^3}\]
Taking cube root of both sides, we get
\[\begin{array}{l} \Rightarrow \sqrt[3]{{64}} = \sqrt[3]{{{a^3}}}\\ \Rightarrow a = 4{\rm{ cm}}\end{array}\]
Therefore, the length of the side of the cube is 4 cm.
Now, let us draw the diagram to show how the resulting cuboid looks.

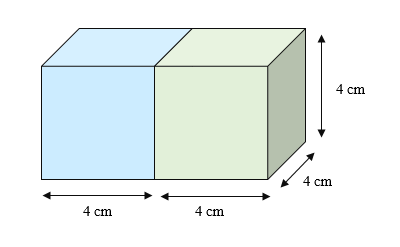
We can observe that when the two cubes are joined together end to end, the breadth and height of the resulting cuboid is 4 cm.
The length of the cuboid is the sum of the lengths of the sides of the two cubes.
Therefore, the length of the cuboid \[ = 4 + 4 = 8{\rm{ cm}}\].
Now, we will find the surface area of the resulting cuboid.
The total surface area of a cuboid is given by the formula \[2\left( {lb + bh + lh} \right)\], where \[l\] is the length, \[b\] is the breadth, and \[h\] is the height.
Substituting \[l = 8\] cm, \[b = 4\] cm, and \[h = 4\] cm in the formula, we get
Surface area of the resulting cuboid \[ = 2\left( {8 \times 4 + 4 \times 4 + 8 \times 4} \right){\rm{ c}}{{\rm{m}}^3}\]
Multiplying the terms in the parentheses, we get
Surface area of the resulting cuboid \[ = 2\left( {32 + 16 + 32} \right){\rm{ c}}{{\rm{m}}^3}\]
Adding the terms in the parentheses, we get
Surface area of the resulting cuboid \[ = 2\left( {80} \right){\rm{ c}}{{\rm{m}}^3}\]
Multiplying 2 by 80, we get
Surface area of the resulting cuboid \[ = 160{\rm{ c}}{{\rm{m}}^3}\]
Therefore, the surface area of the resulting cuboid is 160 cubic centimetres.

Note: We need to keep in mind that the words “surface area” refer to the total surface area, and not the curved/lateral surface area, unless specified. We might make a mistake by calculating the curved surface area instead of the total surface area using the formula \[2h\left( {l + b} \right)\].
We need to also understand that the \[64 {\rm{c}}{{\rm{m}}^3}\] is the volume of both the cube and not the volume of just one cube. If we take it as the volume of one cume then it will be wrong.