Question

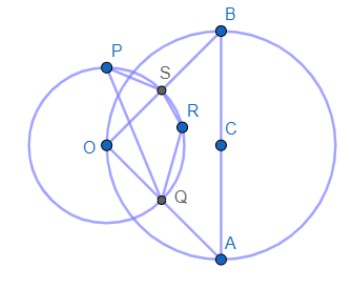
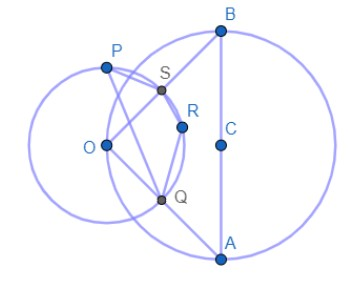
(1) ‘O’ is the centre of circle ${{C}_{1}}$ and AB is the diameter of circle ${{C}_{2}}$ . Quadrilateral PQRS is inscribed in the circle with centre O. Find $\angle QRS$.

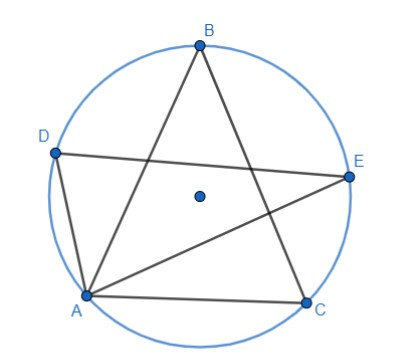
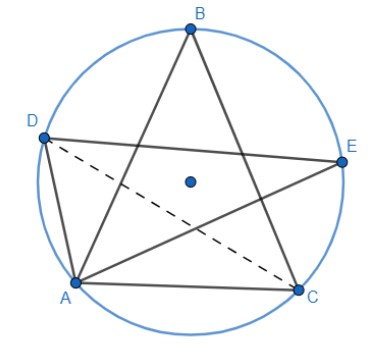
(2) In figure $\angle ADE$ and $\angle ABC$ differ by $15{}^\circ $ , find $\angle CAE$ .

Answer 1

Hint: For solving both the questions you need to use the property that the angles in the same segment of the circle are equal, and angle subtended by a segment of the circle at the centre of the circle is twice the angle subtended by the segment at the circumference of the circle.

Complete step-by-step answer:
Now let us start the first question by making its diagram.

Now using the theorem that the angle at the semi-circle is equal to $90{}^\circ $ .
$\therefore \angle AOB=90{}^\circ $
Now applying the theorem that angle subtended by a segment of the circle at the centre of the circle is twice the angle subtended by the segment at the circumference of the circle, we get
$\angle QPS=\dfrac{1}{2}\times \angle AOB=\dfrac{1}{2}\times 90{}^\circ =45{}^\circ $
Now we know that the sum of opposite angles of a cyclic quadrilateral is $180{}^\circ $ .
$\therefore \angle QPS+\angle QRS=180{}^\circ $
$\Rightarrow \angle QRS=180{}^\circ -45{}^\circ =135{}^\circ $
Now to start with the second question, we draw the diagram with all the required construction.

It is given that in the figure $\angle ADE$ and $\angle ABC$ differ by $15{}^\circ $ . This can be mathematically represented as:
 $\angle ADE-\angle ABC=15{}^\circ $
Now we know that angle ADC is equal to angle ABC, as they are angles subtended by the same segment AC. Also, from the figure, we can see that it is equal to angle ADE. So, we get
$\angle ADC+\angle CDE-\angle ABC=15{}^\circ $
$\Rightarrow \angle CDE=15{}^\circ $
Also, $\angle CDE$ and $\angle CAE$ lie on the same segment, so they are equal.
$\therefore \angle CDE=\angle CAE=15{}^\circ $

Note: Remember that the theorems related to cyclic quadrilateral are not valid for any regular quadrilateral. Also, it is prescribed to learn all the basic theorems related to circles as they are regularly used in the questions related to circles and cyclic quadrilaterals, as we did in the above question.