




How to Calculate and Use the Square Root of 42 in Maths
The square root of a number can be in the form of a natural number or decimal or radical. It depends upon the given number; if it is a perfect square, the square root will be a natural number and if the given number is not a perfect square, the square root will be in the form of a decimal or radical. The square root of 42 will be in the form of a decimal or radical as 42 is not a perfect square. We will use long division and prime factorization to find the square root of 42.
Square root of 42 in Decimal = 6.4807
Square root of 42 in Radical = \[\sqrt {42} \]
The square root of 42 without actual multiplication = 6.461
What is the Square Root of 42?
The square root of 42 is a number when it is multiplied by the number itself gives us 42. The symbol of representation of the square root is “\[\sqrt {} \]”, so we can represent the square root of 42 as\[\sqrt {42} \]. Let’s take the square root of 42 as “x”.
Hence, \[\sqrt {42} = \sqrt {x \times x} \].
The value of \[\sqrt {42} \] or we can say the square root of 42 is 6.4807.
In the radical form, we can write a square root of 42, which can not be reduced further.
In the exponential form, we can write the square root of 42 as \[{42^{\dfrac{1}{2}}}\].
- Square root of 42 is an irrational number as it cannot be expressed in the form of the \[\dfrac{p}{q}\].
Prime Factorization Method to Find the Square Root of 42
For the Prime factorization method, first we have to find the prime factors of 42 and then the square root of 42.
Prime factors of 42 = 2, 3, & 7
\[42=2\times 3\times 7\] and prime factors of \[\sqrt {42} = \sqrt 2 \times \sqrt 3 \times \sqrt 7 \]
And we know the value of
\[\sqrt 2 \]=1.414
\[\sqrt 3 \]=1.732
\[\sqrt 7 \]=2.646
Therefore, \[\sqrt {42} = 1.41 \times 1.732 \times 2.646\]
Long Division Method to Find Square Root of 42
Now we will do the long division method to find the square root of 42.
Step 1 : First we start pairing the digit by the right side, we have only one pair, i.e., 42.
Step 2 : Now take a number ‘a’ such that \[a\times a \le 42\], here a will be 6 then \[6\times 6=36 \le \] 42.
Step 3 : We can see that both quotient and the remainder are 6. Now double the divisor and it is 12.
Step 4: Now put the decimal in both dividend and quotient and 3 pairs of 0 in the dividend part after the decimal.
Step 5: Bring down one pair of 0 and the dividend becomes 600 now. Find a number such that \[12\times 10+a \times a \le 600\]. The number will be 4 as \[124 \times 4= 496 \leq 600\].
Step 6: Now repeat the above step for the remaining two pairs of zero.

Long Division for Square Root 42
Here is how we get the square root of 42, i.e., 6.480 by using the long division method.
Find the Square Root of 42 without Actual Multiplication
Finding square root without actual multiplication is also called an approximation method to find square root. Let’s take two consecutive perfect square numbers in which the given number 42 lies. The two numbers will be 36 \[\left( {{6^2}} \right)\]and 49 \[\left( {{7^2}} \right)\]
Clearly, the whole number part of the square root of 42 is 6 and for the decimal part of the square root, we will use the below formula:
\[\dfrac{\left(\text{Given number} - \text{smaller perfect square number}\right)}{\left(\text{greater perfect square number} - \text{smaller perfect square number}\right)}\]
=\[\dfrac{{42 - 36}}{{49 - 36}}\]
\[ = \dfrac{6}{{13}}\]
=6.461
Hence, we get the square root of 42 as 6.461 without actual multiplication.
Repeating Subtraction Method
This method will subtract successive odd numbers up to 42. This process will go until we get 0 as a result. The number of steps is the square root of the number.
Step 1: 42 – 1 = 41
Step 2: 41 – 3 = 38
Step 3: 38 – 5 = 33
Step 4: 33 – 7 = 26
Step 5: 26 – 9 = 17
Step 6: 17 – 11 = 6
We will not get 0 in this process. So, the square root of 42 lies between 6 and 7.
Location of Square Root on the Number Line
Estimation method: We will plot a non-perfect square on the number line in this method.
We know that \[{6^2} = 36\] and \[{7^2} = 49\].
Plot all integers from 36 to 49 on the number line.
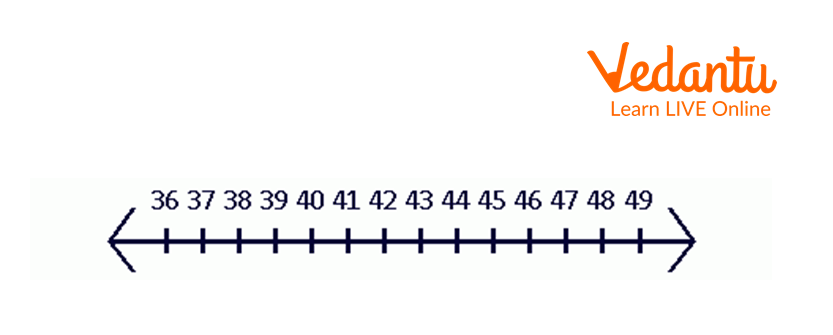
Number Line
Now find the midpoint.
The midpoint is \[\dfrac{{49 - 36}}{2} = 6.5\] units away from 36.
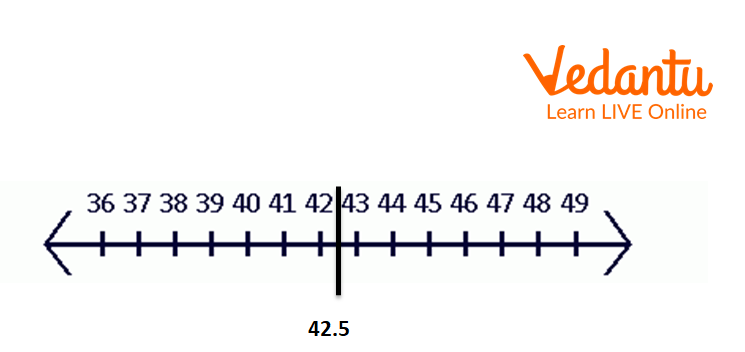
Midpoint for the Interval 36 to 49
The mid-point is 42.5.
Now take the square roots of all numbers.
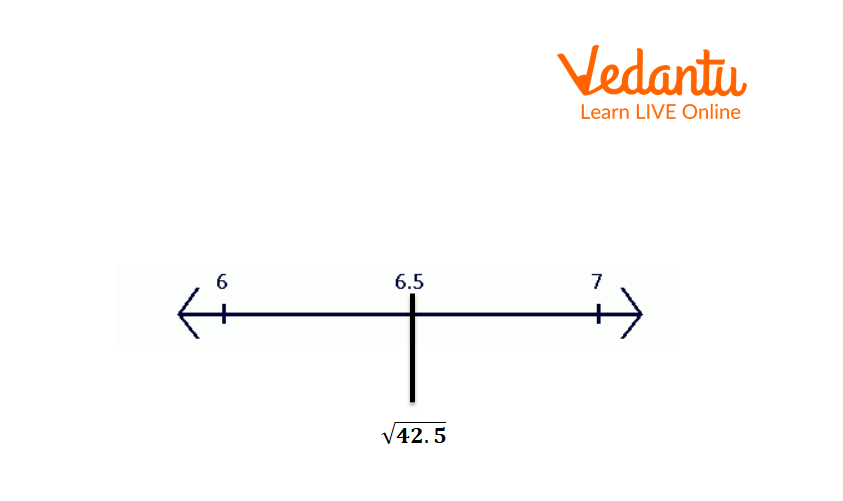
Square Root of 42 on the Number Line
The square root of 42 lies near 6.5 on a number line.
Interesting Facts
The square of square root is a number of a number that is the same number.
A perfect square root exists for a perfect square number.
The square roots of 0 and 1 are 0 and 1, respectively.
Solved Examples
1. Find the square root of 144 by prime factorization method.
Solution: To find the square root of 144 by the prime factorization method, first we have to find prime factors of 144.
\[144=2\times2\times 2\times 2\times 3\times 3\]
\[\sqrt {144} = \sqrt {2 \times 2 \times 2 \times 2 \times 3 \times 3} \]
= \[2\times2\times3\]
= 12
So, the square root of 144 is 12.
2. How much should be added in 42 to make it a perfect square?
Solution: A perfect square is a number whose square root is always a natural number.
Here, we asked how much should be added to 42 to make it a perfect square, the nearest perfect square to 42 is 49, to make it 49 we add 7 in 42.
Hence, 7 should be added to 42 to make it a perfect square.
3. Write the square of 42.
Solution: To find the square of 42, we multiply it by itself i.e. 42.
Hence, the square of 42 = 42 \[ \times \]42
= 1764
Therefore, the square of 42 is 1764.
Practice Question
1. What is the square root of 42.5?
Ans: 6.5
2. What is the square root of 41?
Ans: Approx. 6.4031.
Summary
In this article, we have learned how to find the square root of 42 using the long division method, repeated subtraction method, and without actual division. The square root of 42 is a number, which when multiplied by itself results in the original number 42. The square root of 42 is an irrational number since the value of square root 42 cannot be expressed in the form of $\dfrac{p}{q}$.
FAQs on Square Root of 42 Explained for Students
1. Is the square root and square of a number the same thing?
The square root of a number is written in the form \[{a^2}\] and the square root of a number is written in the form \[\sqrt a \]. To get a square number, we multiply the number by itself.
The square root of a number is a number such as the product of the number and itself is a given number. Square root is the inverse operation of square.
For example: The square of 9 is \[{9^2} = 81\]
The square root of 9 is \[{9^2} = 81\]
2. If the sum of the square of two numbers is a perfect square, then what is the name of the group of three numbers?
Ans: Assume a, b, and c are three numbers such that
\[a^{2}+b^{2}=c^{2}\]
Then a, b, and c are known as Pythagorean triples.
If the sum of the square of two numbers is a perfect square, then the name of the group of three numbers is Pythagorean triples.
3. What is the square root of a negative number?
Ans: Assume that
\[x = \sqrt { - a} \]
Taking square both sides,
\[{x^2} = - a\]
We know that square of a positive number or negative number is always a positive number.
Thus, \[{x^2} = - a\] is not possible. Thus, our assumption is wrong.

















