Scaling in Math

Have you ever clicked a photo using mobile or any camera? What do you see? An image, right. This image represents the object that you clicked. But, can you tell me whether the size of the image clicked and the original size is equal? No. It is so because you have either scaled-up or scaled-down the object size. Representation of an image or object by enlarging or shrinking is called ‘scaling’ of the image or object.

What is Scaling in Math?

Scaling is the factor which is used to represent the object size. The size of the object can be shown by increasing or decreasing its original size. In general, the represent size of the object increased for the small object whereas it decreased for the bigger object. Scaling is used for better viewing of an object. The ratio by which an object’s size increased or decreased is called as scale factor.

What is a Scale Factor?

Scale factor is the ratio between corresponding measurement of an object and representation of that object. The scale factor is a whole number or greater than 1 to make a larger copy. The scale factor is a fraction or less than 1 to make a smaller copy. Therefore, scale factor can be expressed by any number or fraction. Also, scale factor can be expressed using colon (:), such as

Original sized object : Representation sized object

where, Representation sized object = Any number x Original sized object (in case of larger copy)

or, Representation sized object = \[ \frac{1}{Any \, number} \] x Original sized object (in case of smaller copy)

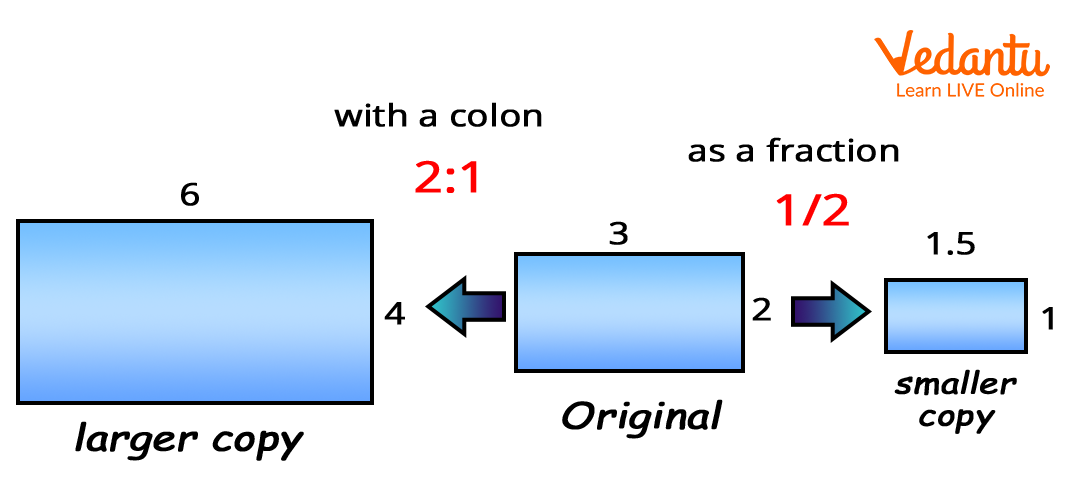
Scale factor

Types of Scale Factor

There are two types of scale factor:

1. Scale-up Factor

2. Scale-down Factor

1. Scale-up Factor: To show the larger size of a small-sized object, we multiply by a number to the original size of the object. In this case, we multiply with the a number greater than 1 to the original sized object. To find the scale-up factor, we used the following formula:

Scale - up (Smaller to larger) = {Larger figure measurement} ÷ {Smaller figure measurement}

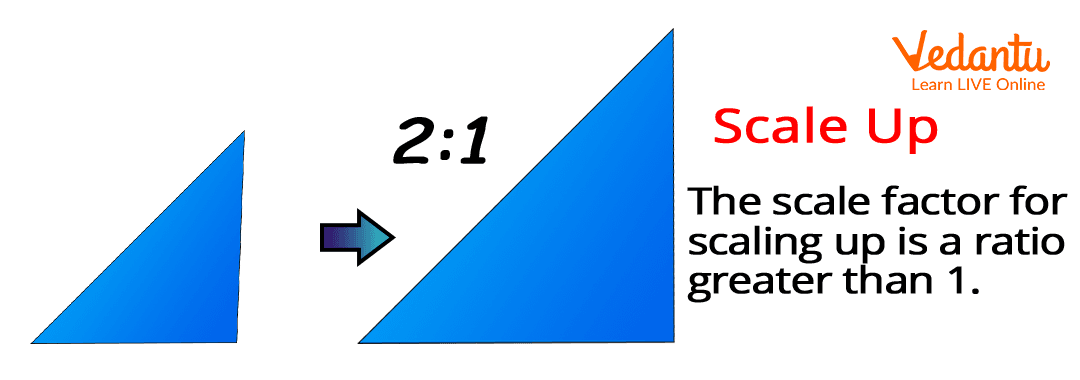
Scale Up

2. Scale-down Factor: To show the smaller size of a bigger-sized object, we divide by a number to the original size of the object. In this case, either we multiply with a number smaller than 1 or divide it by a number greater than 1 to the original sized object. To find the scale-down factor, we used the following formula:

Scale - down (larger to Smaller) = \[ \frac{Smaller \, figure \, measurement}{Larger \, figure \, measurement} \]

Scale down

Scaling in Geometry

In Geometry, scale factors can be obtained from similar figures, or we can create another image using the scale factor over the original figure.

Example of Scaling in Geometry: In this example, we show the scale-up factor. Here, a scale factor of 2 is shown, which means that the new figure obtained will be twice the original figure. All the sides of the triangle multiplied by 2 to obtain the new figure.

Scale factor of 2

Why 2? Lets see the above given figure. In the first figure, we can observe that value of base, height and hypotenuse are equal to 8, 6 and 10 respectively. In the second figure, values of these are 16, 12 and 20. Comparing both the figures, we can calculate scale factor as:

\[ Scale Factor = \frac{Base \, Measurement \, of \, New \, Figure}{Base \, Measurement \, of \, Old \, Figure } = \frac{16}{8} = 2 \]

\[ Scale Factor = \frac{Height \, Measurement \, of \, New \, Figure}{Height \, Measurement \, of \, Old \, Figure} = \frac{12}{6} = 2 \]

\[ Scale Factor= \frac{Hypotenuse \, Measurement \, of \, New \, Figure}{Hypotenuse \, Measurement \, of \, Old \, Figure} = \frac{16}{8} = 2 \]

Hence, the scale factor is 2.

Now, let us consider another example to understand it more.

Example: What is the scale factor from ΔABC to ΔDEF?

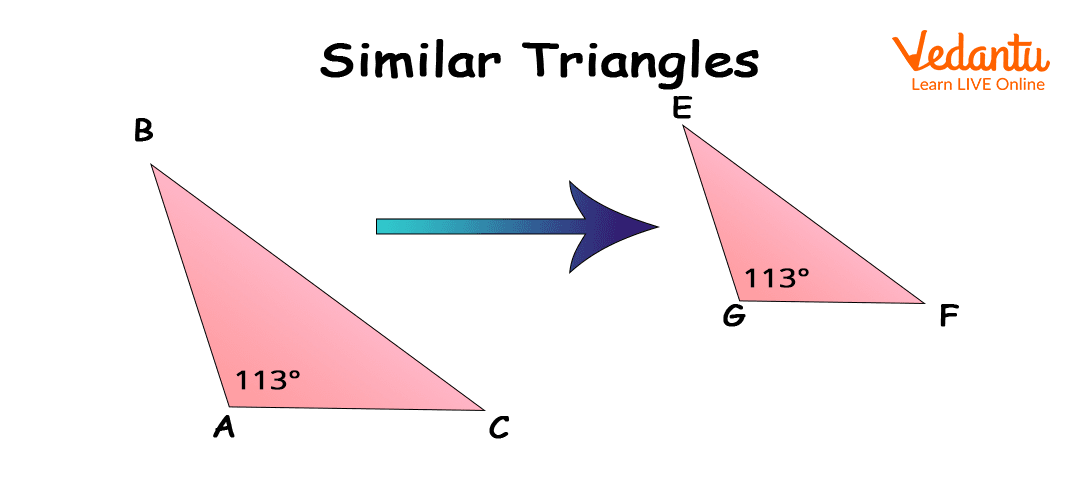
How to find the scale factor?

From the above-given figures, we can easily observe that the values of all sides are decreasing. So, here we need to find the scale-down factor. The point to be noted is that we can find the scale factor using the ratios of respective sides/same sides of both the triangles.

\[ Scale Factor= \frac{Measurement \, of \, Side \, EF (New \, Figure)}{Measurement \, of \, Side BC (Old \, Figure)} = \frac{12}{18} = 0.66666 \]

Remember: We can find the scale factor of an image using the values of corresponding sides, angles and diagonals.

Conclusion

From this article, we have learnt the meaning of scaling and types of scale factor. We also learn how to find the value of scale factor. To know more mathematical terms, visit our website.