How to Apply the Pythagorean Theorem in Real-World Math Problems
The Pythagoras Theorem applied in a right-angled triangle states that the square of the side hypotenuse will be equal to the sum of the squares of the base and the perpendicular.
Let's solve some questions for further understanding -
Questions:
Identify the length of hypotenuse in the given triangle -
Image - An Image of a Triangle
Pythagoras' theorem is applicable in which kind of triangles?
Solve for an in the given triangle -
Image - An Image of a Triangle
Is the given figure a right-angled triangle ?
Image - An Image of a Triangle
Find the value of the missing side.
Image - An Image of a Triangle
Find the length of the hypotenuse.
Image - An Image of a Triangle
Use Pythagorean Theorem to check whether the given triangle is a right-angle triangle or not.
Image - An Image of a Triangle
Is the following Pythagorean Triplet correct?
3, 5 and 7
Solve for c in the given triangle -
Image - An Image of a Triangle
In the below given right triangle, find the value of y.
Image - An Image of a Triangle
In a right triangle, the longest side is 8 cm. One of the remaining sides is 4√3 cm long. Find the length of the other side.
What is the value of the missing side of the triangle?
Image - An Image of a Triangle
ABC is a right triangle. AC is its hypotenuse. The length of side AB is 2√5. Side BC is twice side AB. Find the length of AC.
Find the value of x.
Image - An Image of a Triangle
Is ∆ABC a right-angled triangle, where AB = 5cm, BC = 10cm, AC = 15cm?
Answers -
7.2, the length of the hypotenuse in the given triangle is 7.2.
Pythagoras theorem is applicable only in right-angled triangles.
Given, b=12 and c= 15
a2+b2=c2
a2+ 144 =225
Subtract 144 from each side to get:
144 - 144 + a2 = 225 - 144
a2 = 225 - 144 ⇒ a2 = 81
⇒ a = √81
a = 9
Yes, the given triangle is a right angled triangle.
By Pythagoras theorem, a2+b2=c2
Let b=9 c=12
144 - 81 =a2 ⇒ 63 = a2
√63 = a
Therefore, the length of the missing side is √63.
10in.
By Pythagoras theorem, a2+b2=c2
Let a=6 b=7 c=9
36 + 49 = 81 ⇔ 9 x 9 = 81
Therefore, LHS≠RHS
Hence, the given triangle is not a right angle triangle.
By Pythagoras theorem, a2+b2=c2
Let a=3 b=5 c=7
9 + 25 = 34
7 × 7 = 49
Therefore, LHS≠RHS
Hence, 3, 5 and 7 are not correct Pythagorean triplets.
Given, a=11 b=15
By Pythagoras theorem,
a2+b2=c2
121 + 225 = c2
346 = c2
c = √346m
By Pythagoras theorem we get,
z2=x2+y2
Now, directly substituting the values
⇒ 169 = 25 + y2
⇒ y2 = 144 ⇒ y = 12
Hence, the value of y is 12.
4cm.
By Pythagoras theorem, a2+b2=c2
Let a=3 b= 6
9 + 36 = c2 ⇒ 45 = c2
√45 = c
Therefore, the length of the missing side is √45cm.
AC = 10
By the pythagoras theorem, Hypotenuse2 = Base2 + Perpendicular2
x2 = 64+36 = 100
x = 10
Therefore, the value of x is 10.
If ∆ABC is a right-angled triangle, then AB2+BC2=AC2
AB = 5, BC =10, AC = 15
AB2 + BC2 = 25 + 100 = 125
AC2 = 225
Since, AC2 ≠ AB2 + BC2
Hence, ABC is not a right-angled triangle.
Importance of Pythagoras Theorem Worksheet for Students
Students of KG-3 will be able to gain a better understanding of the Pythagoras Theorem from these worksheets. From these questions, students will learn how to find the different sides of the right-angled triangle. The Pythagoras theorem topics have been explained in the worksheets to understand the students better. Not just that, but there are different types of sums, such as word problems, real-time applications, numerical questions, and so much more. Students will also find MCQ on Pythagoras' Theorem in these worksheets.
Students who want to complete their KG-3 Maths syllabus properly need to download these worksheets and their solutions in the first place. This will not only help them understand the examination pattern but will also improve their answering skills as well. The more they practice the questions provided here, the better it will be for their minds. Students can develop great logical thinking and cognitive abilities by solving the questions provided in these worksheets. Downloading the Pythagoras theorem sums and worksheets will help them score good marks in the examinations.
Benefits of Pythagoras Theorem Questions and Worksheets
For students who are in Class KG-3, it is extremely important to complete their syllabus. Thus they can take some help from the questions provided in the worksheets related to the Pythagoras theorem and understand the chapter completely.
These worksheets have been prepared by the learned subject matter experts at Vedantu and contain all the details about the chapter. The experts have also included some special tricks and shortcuts to solve the problems easily.
Students can download and refer to the worksheets to resolve any queries or clarify any doubts that they might have about the chapter. This will enable them to boost their preparation for the examination best.
Students will also be able to answer questions independently after practising from these worksheets. They will understand the answering pattern with the help of the Pythagoras Theorem Worksheets PDF and can answer questions on their own.
Download Worksheets for Pythagoras Theorem Questions
To learn the concepts of Pythagoras' theorem best, download and practice Pythagorean Theorem Worksheet from Vedantu. These study materials are highly reliable and will help you understand the topics in the best way. Prepare well for your exams with these worksheets.
FAQs on Pythagorean Theorem Worksheet: Step-by-Step Practice
1. What is the Pythagorean Theorem?
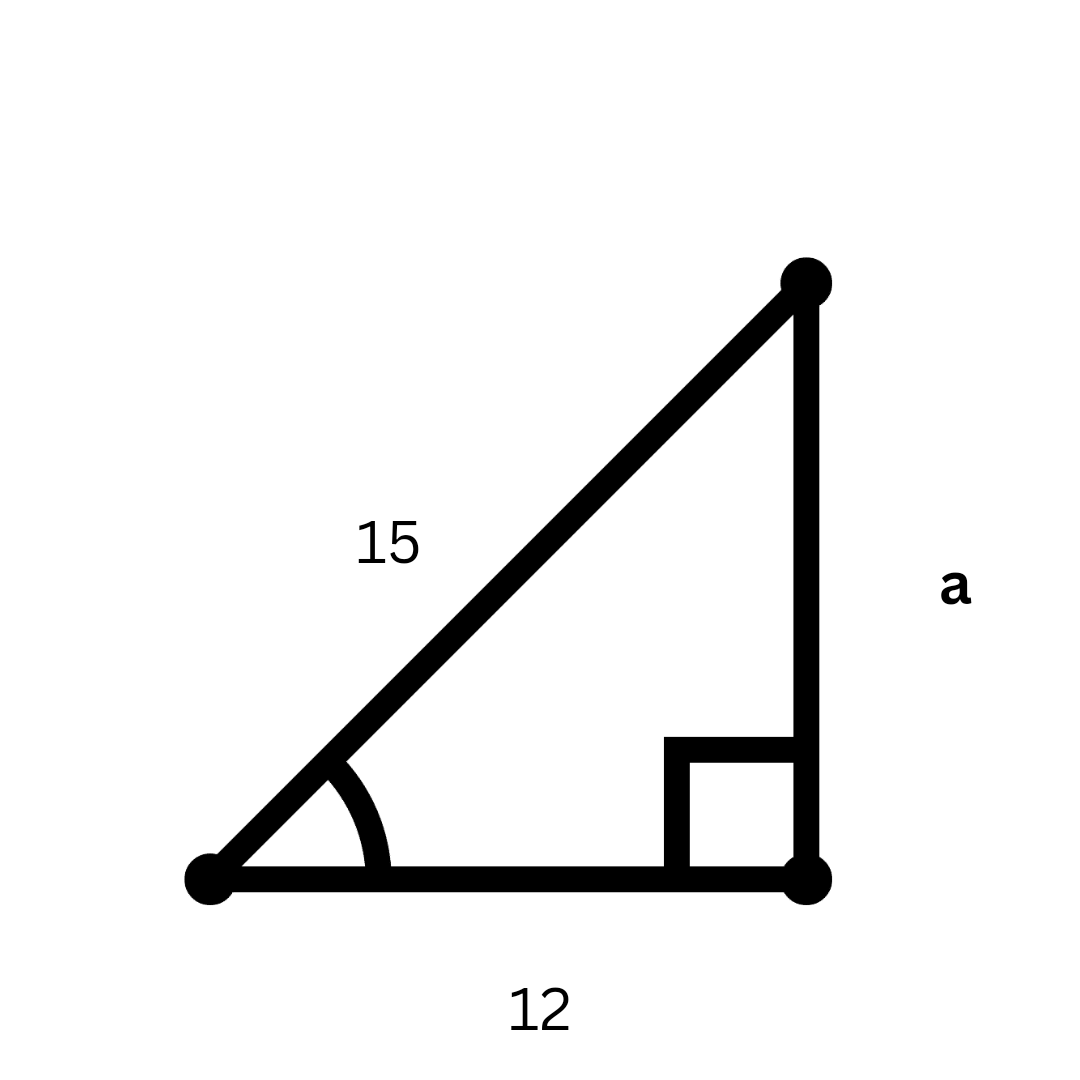
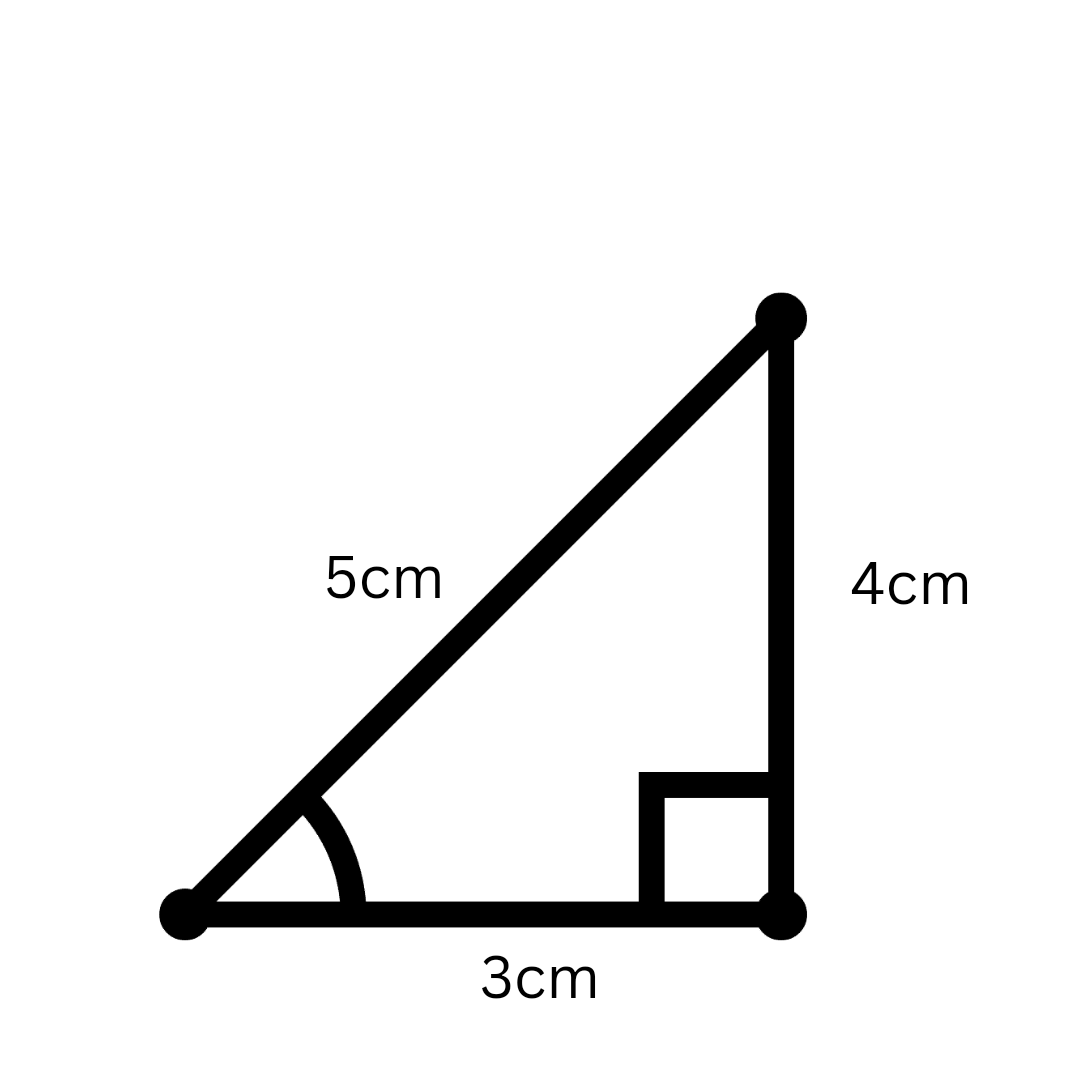
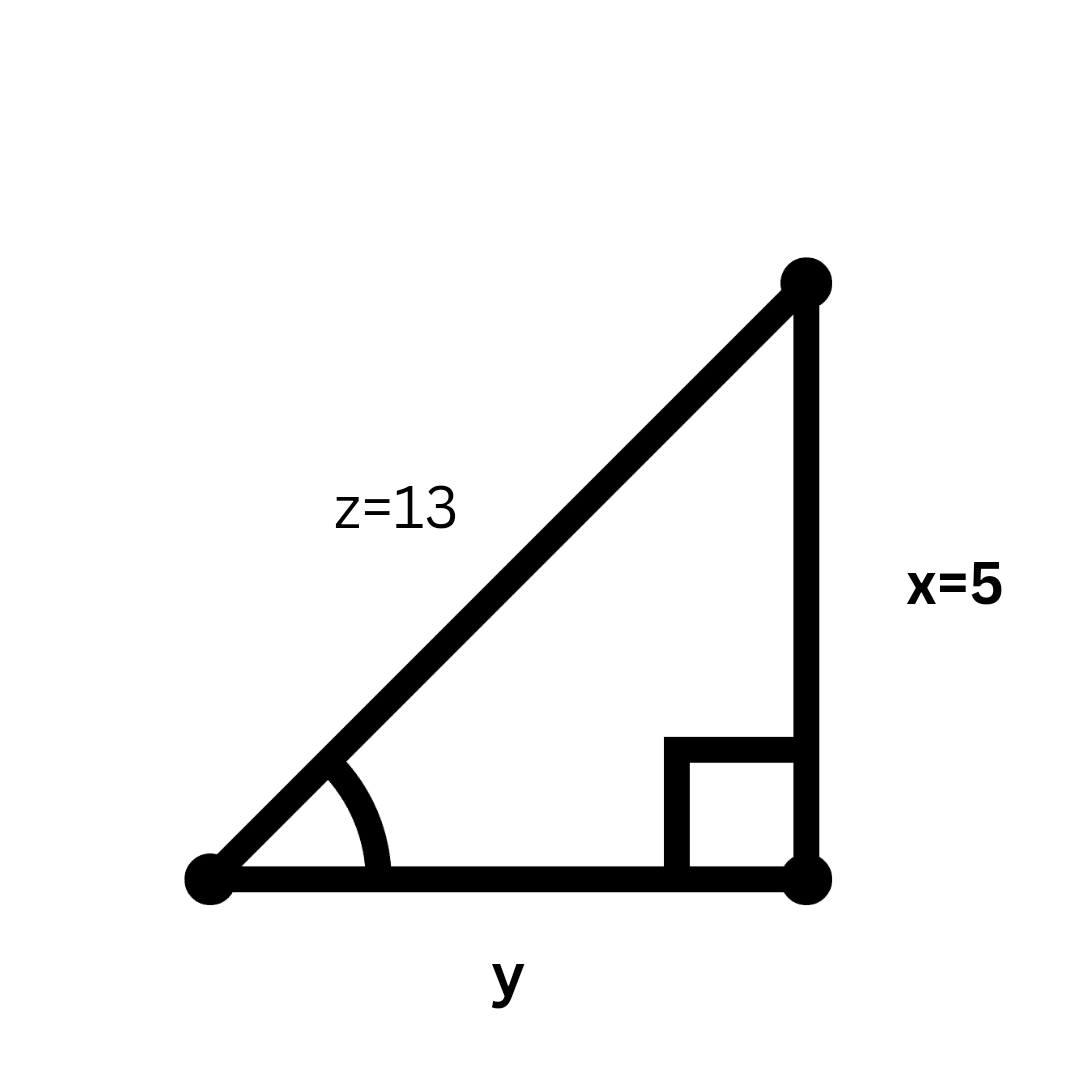
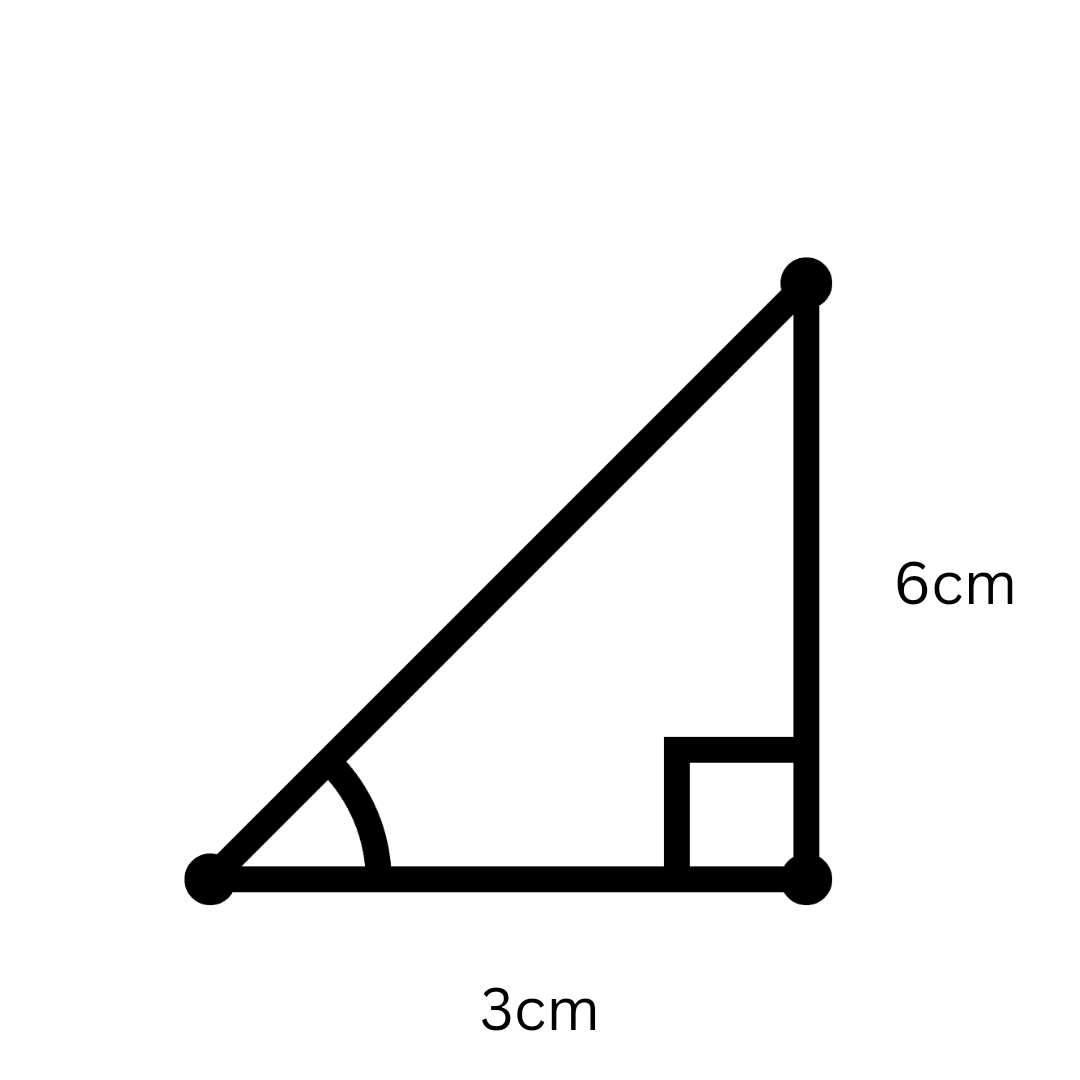
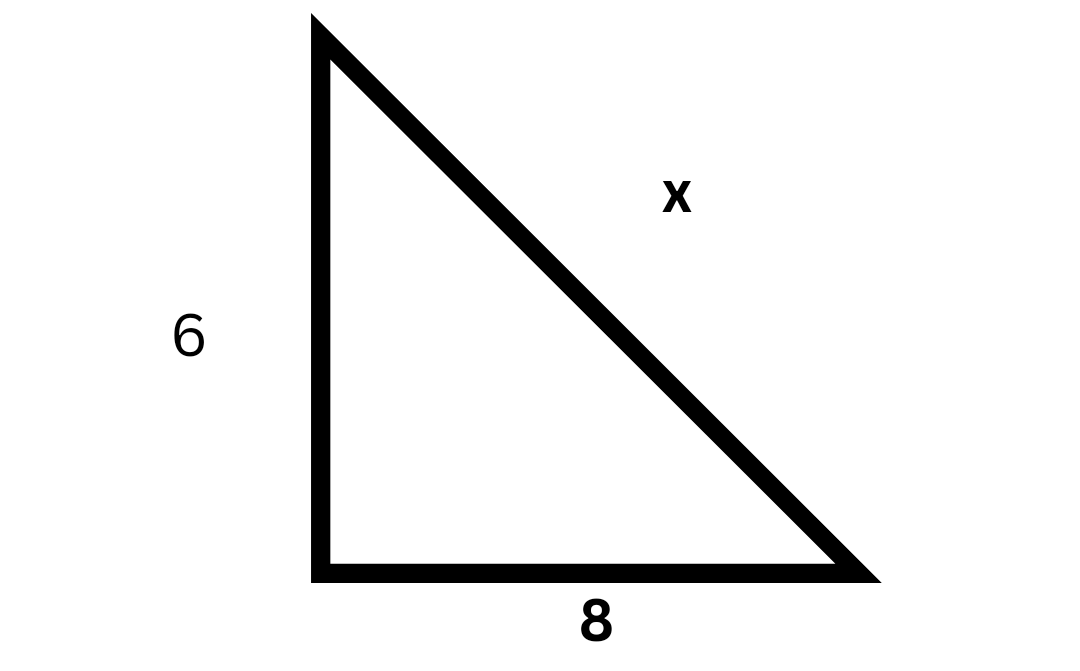
The Pythagorean Theorem is a fundamental principle in geometry which states that in a right-angled triangle, the sum of the squares of the two legs is equal to the square of the hypotenuse. The formula is expressed as: $$a^2 + b^2 = c^2$$ where a and b are the lengths of the legs, and c is the length of the hypotenuse. Vedantu's worksheets help students practice applying this theorem to various problems and reinforce their understanding through guided examples.
2. How do you use a Pythagorean Theorem worksheet?
To use a Pythagorean Theorem worksheet effectively, follow these steps:
- Read each question carefully and identify the sides of the right triangle.
- Apply the formula $a^2 + b^2 = c^2$ to solve for the missing side.
- Check for real-life application questions that require drawing or imagining triangles.
- Review your answers to ensure accuracy.
3. What types of problems are included in a Pythagorean Theorem worksheet?
Pythagorean Theorem worksheets from Vedantu typically include:
- Finding the length of a missing side in right-angled triangles.
- Word problems involving real-world scenarios, such as ladders or navigation.
- Questions requiring students to determine whether a triangle is right-angled.
- Problems involving calculations with decimals and integers.
- Challenging puzzles and application-based questions to enhance analytical skills.
4. Why is practicing the Pythagorean Theorem important for students?
Practicing the Pythagorean Theorem is essential for students because:
- It builds a strong foundation in geometric concepts and spatial reasoning.
- It lays the groundwork for advanced mathematics, including trigonometry and coordinate geometry.
- It is frequently used in real-life applications such as construction, engineering, and navigation.
- Regular worksheets reinforce understanding and promote problem-solving skills.
5. How can Vedantu's worksheets help me master the Pythagorean Theorem?
Vedantu's Pythagorean Theorem worksheets are designed to:
- Provide step-by-step solutions and guided examples.
- Include beginner to advanced problems for gradual learning.
- Offer interactive practice through quizzes and live sessions.
- Help students learn effective strategies for solving right triangle problems.
6. What are some real-life examples where the Pythagorean Theorem is applied?
Some real-life applications of the Pythagorean Theorem include:
- Determining the shortest distance between two points (such as across a park).
- Calculating the height of a building using a ladder and a known distance from the wall.
- Finding the length of a diagonal in rectangular objects like televisions or tiles.
- Assisting in navigation and mapping for finding straight-line distances.
7. How do you identify the hypotenuse in a right triangle when using the Pythagorean Theorem?
The hypotenuse is the longest side of a right-angled triangle and is always opposite the right angle. When applying the Pythagorean Theorem, the hypotenuse is represented as c in the formula $a^2 + b^2 = c^2$. Vedantu's expert tutors help students recognize the hypotenuse in various triangle orientations and provide tips for accurate identification.
8. Are there different levels of difficulty in Pythagorean Theorem worksheets?
Yes, Vedantu's Pythagorean Theorem worksheets are tailored to different skill levels.
- Basic worksheets focus on simple calculations and finding one missing side.
- Intermediate worksheets include word problems and decimals.
- Advanced worksheets challenge students with multi-step problems and real-world scenarios.
9. How can students check their answers on Pythagorean Theorem worksheets?
Students can verify their answers on Pythagorean Theorem worksheets by:
- Substituting the values back into the formula $a^2 + b^2 = c^2$ to check for accuracy.
- Reviewing step-by-step solutions provided by Vedantu for common worksheet problems.
- Participating in Vedantu's interactive sessions where educators discuss solutions and common mistakes.
10. What topics should students review before attempting Pythagorean Theorem worksheets?
Before starting a Pythagorean Theorem worksheet, students should review:
- The properties of right-angled triangles.
- Basic operations with squares and square roots.
- Key vocabulary such as hypotenuse, legs, and right angle.
- Methods to classify triangles by their angles.
