




Key Principles of Numeration Explained with Examples
We use a set of digits known as numerals to represent numbers. A few examples of numbers are 1234 2314 56111. Numeration is the process of expressing numbers in words. A number system is described as a logical writing system that uses digits or symbols to represent numbers. In this article, we will discuss numbers and numeration in detail.
Number and Numeration
An arithmetic value used to indicate an amount is called a number. A number is a mathematical concept that is used for counting, measuring and labelling. Thus, Mathematics is built on numbers. Numeration is the process of expressing numbers in words. A number system is described as a logical writing system that uses digits or symbols to represent numbers.

Examples of Numerals
What is Numeration?
Numbers are represented by symbols or groupings of symbols called numerals. Expressing a number in words is called numeration. Numeration systems are organised ways or processes for counting to figure out how many total units are in a collection.
Three functions of numerical systems are identification, ordering and counting. When determining who crosses the finish line first, second or third in a race, for instance, numerical systems can also be used to identify a person's or unit's position in a series.
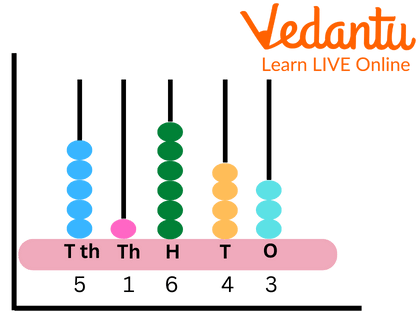
Numeration with Abacus
Difference between Number and Numeral
A number is a measurement or count that, in our minds, is essentially an idea. Numbers are expressed using numerals like "4" or "four" in writing or conversation. However, we might also touch the ground four times or hold up four fingers. These all serve as alternative expressions for the same number.
A numeral is a name or symbol that represents a certain number. Examples are the numerals 3, 49 and twelve. Therefore, the numeral is how we write the number.

Value of a Number
Solved Examples
Example 1: Which number will be produced by adding one to :
(i) 9
(ii) 99
Ans: (i) We will get 10 if 1 is added to 9.
(ii) If 1 is added to 99, we will get 100.
Example 2: Write the following in descending order:
(i) 308, 312, 306, 318
(ii) 513, 515, 510, 525
Ans: As we know that information is considered to be in descending order if it is arranged from highest to lowest.
(i) 318, 312, 308, 306
(ii) 525, 515, 513, 510
Example 3: Write the numbers that are both bigger and less than the specified number:
(i) More than 539 but less than 544
(ii) Less than 999 but more than 994
Ans: (i) A number which is more than 539 and less than 544 is 541.
(ii) A number which is less than 999 and more than 994 is 996.
Conclusion
The technique of representing a number in digits or figures is known as notation. Numeration is the process of representing numbers in words. We have learned about numbers and numeration in detail in this article. We have also provided some solved examples to understand the topics better.
FAQs on Numeration: Concepts, Methods & Practice
1. What is numeration in Maths?
Numeration is the method of representing numbers in words. It is a system of reading and writing numbers using a specific set of rules. For example, the numeral '5' is written as 'five' in words, and this process of expressing it is called numeration.
2. What are the two main systems of numeration?
The two primary systems of numeration used to read and write large numbers are:
- The Indian System of Numeration: This system uses place values like Ones, Tens, Hundreds, Thousands, Lakhs, and Crores. Commas are used to separate periods of thousands, lakhs, and crores (e.g., 5,43,210).
- The International System of Numeration: This system uses place values like Ones, Tens, Hundreds, Thousands, Millions, and Billions. Commas are placed after every three digits from the right (e.g., 543,210).
3. How do you write the number 8,43,105 using both Indian and International systems of numeration?
Here is how to write the number 8,43,105 in words using both systems:
- Indian System: Eight Lakh, Forty-Three Thousand, One Hundred Five.
- International System: Eight Hundred Forty-Three Thousand, One Hundred Five.
4. What is the key difference between numeration and notation?
The key difference lies in the format of representation. Numeration is the method of expressing a number in words (e.g., 'Two Hundred Fifty-Three'). In contrast, notation is the method of representing a number in figures or digits (e.g., '253').
5. How does understanding place value help in numeration?
Place value is fundamental to numeration because it assigns a unique value to a digit based on its position within a number. For instance, in the number 444, the first '4' from the right represents 4 ones, the second represents 4 tens (40), and the third represents 4 hundreds (400). Without understanding place value, we could not correctly read or write the number as 'Four Hundred Forty-Four'.
6. Why are commas important in numeration systems?
Commas act as separators for different periods (like thousands, lakhs, or millions), making large numbers easier to read and pronounce correctly. They help visually group the digits according to the rules of a specific numeration system (Indian or International), preventing errors in reading a number like 1234567 as 'One Crore Twenty-Three Lakh...' versus 'One Million, Two Hundred Thirty-Four Thousand...'.
7. What is the largest 4-digit number and how is it written in words?
The largest 4-digit number is 9999. Using the system of numeration, it is written in words as 'Nine Thousand, Nine Hundred Ninety-Nine'.
8. Can Roman numerals be considered a system of numeration?
Yes, Roman numerals (I, V, X, L, C, D, M) are a system of notation, and the method of reading them is a form of numeration. However, it is a non-positional system, meaning the value of a symbol does not change with its position, which makes it different from the Hindu-Arabic system that relies on place value.























