Identifying Inputs and Outputs in Math Functions

In mathematics, the concepts of input and output are related to functions. A function's input and output are both variables subject to change. In simple mathematical terms, The input goes into the function, and the output is something that the function produces. Input and Outputs can also be defined as inputs are things you put in, use, or operate, while outputs are things you make, provide, or supply. For Example, x is the input parameter, and y is the output parameter in the function y = x + 9. The function operates by converting an input value, such that x = 10, into an output value of y = 19 which is the result of changing the value of x in the equation y = x + 9 to 10. The output value is 19. It is important to remember that each input has a single output in a function. In this article, we will learn about what input means in math and its examples.

Input and Output in Mathematics

So now the question arises, what does input mean in math? Inputs are the variables or things that are put in, used, or operated inside a function to obtain an output. Inputs are generally termed independent variables or parameters.

Whereas output math definitions are defined as the parameters or things produced by the function. Since outputs depend on the value of the input, the output is occasionally referred to as the dependent variable.

Process of Input and Output

For Example: Y = 5x + 3

Here, x is the input, the term (5x + 3) is the process, and x is the output.

Rules for Functioning of Input and Output

In simple terms, the input goes into the function, and the output comes out of the function. In the function y = x + 5, the x is the input variable and the y is the output variable. The function takes an input value, x = 3, for example, and produces an output value.

Graphs, Tables, and Algebraic expressions are the three most typical formats for expressing functions.

Graphs

On a graph representing a function, the input values run along the bottom, and the output values run down the left.

There are different input and output values for each point on the graph.

For Example Plot points to create a graph of equation f(x): x - 2y = 2.

Select input values first. Let's use multiples of 3 as the input values, as this function contains a fraction with a denominator of 3. We'll go with 0, 3, and 6. Use the output value to figure out the coordinate pairs by evaluating the function at each input value.

For x = 2, f(2) = $2 - 2(y)$= 2 ⇒ (2, 0)

For x = 4, f(4) = $4 - 2(y)$= 2 ⇒ (4, 1)

For x = 0, f(0) = $0 - 2(y)$= 2 ⇒ (0, -1)

For x = -2, f(-2) = $-2 - 2(y)$= -2 ⇒ (-2, -2)

Draw a line between the points and plot the coordinate pairs. The function f(x) = $x - 2y = 2$ is displayed in the graph below.

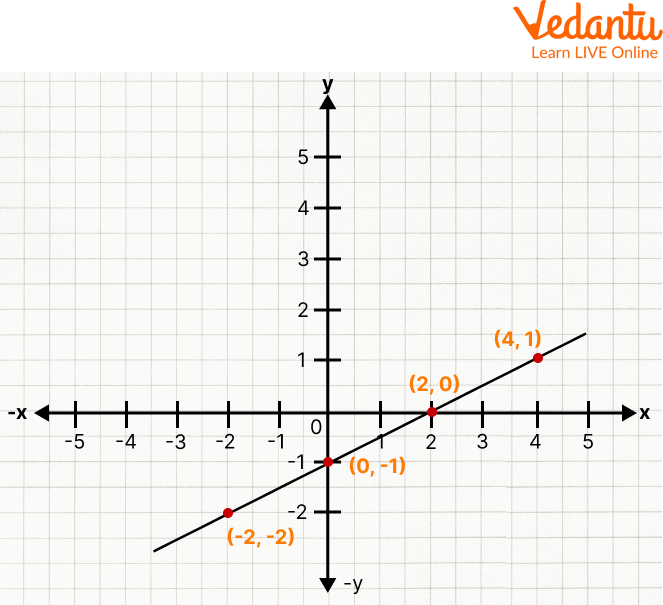
Graphical Representation of Points

Tables

When a function is shown as a table, the table typically has two columns: an inputs column and an outputs column. A 3rd column can be added between the input and output to display the input outcomes in the function's output.

For Example, We have taken a simple function f(x) = 2x + 4

This table displays the inputs 0, 1, 2, 3, 4, and 10. The table displays the following outputs: 4, 6, 8, 10, 12, and 24. It should be noted that each input only results in one output, and the value of the output depends upon the input's value.

Algebraic Expressions

What do you mean by algebraic expressions? The terms of an algebraic expression are combined using operations like addition, subtraction, multiplication, division, etc. Consider the equation 10x + 3 as an example. Thus, 10x + 3 can be considered an algebraic expression.

Examples:

• $3 y^2 x-2 y x^2$

• $(a-7 b)^3+2 a+b$

• $91 m+6 n+1$

An algebraic expression is composed of various parts. Let's look at the graphic below to understand better any algebraic equation's concepts of Variables, Constants, Terms, and Coefficients.

Algebraic Expression

Input and Output Math Examples

Example 1: What rules were used to get the following table?

$y = 3x + 4$

Ans: Remember that x is the input and y is the output. We must examine the input/output or $\dfrac{x}{y}$ pairings in the various equations to see which rule was used to produce the table.

Test the first pair with the values x = 1 and y = 7. Put this in the first equation as a replacement.

$y = 3x + 4$

$7 = 3(1) + 4$

$7 = 3 + 4$

$7 = 7$

Since this works, the equation could be correct. But as of now, we're still determining.

Test the second pair with the values $x=2$ and $y=10$. Put this in the first equation as a replacement.

$y=3 x+4$

$9=3(2)+4$

$9=6+4$

$9=10$

This isn't right, hold on.

Therefore, this was not the rule used to make the table.

Test the first pair with the values x = 3 and y = 13. Put this in the first equation as a replacement.

$y = 3x + 4$

$13 = 3(3) + 4$

$13 = 9 + 4$

$13 = 13$

Since this works, the equation could be correct. But as of now, we're still determining.

Test the first pair with the values x = 4 and y = 16. Put this in the first equation as a replacement.

$y = 3x + 4$

$16 = 3(4) + 4$

$16 = 12 + 4$

$16 = 16$

Since this works, the equation could be correct. But as of now, we're still determining.

Example 2: Calculate the value of x in the following equation: $3x + 2 = 20$

Ans: The provided equation is $3x + 2 = 20$.

Separate the constants and the variables;

The constants can stay on the RHS, and the variable can stay on the LHS.

$3x = 20-2$

Subtract the constants;

$3x = 18$

The variable's coefficient is divided by both sides;

$x = \dfrac{18}{3}$ = 6

As a result, x has a value of 6.

Example 3: Combine the algebraic expressions 5x + 1 and 3y + 8z + 9.

Ans: To add two algebraic expressions, we combine similar terms. On adding, 5x + 1 + 3y + 8z + 9. If the terms are rearranged, we obtain the total as 5x + 3y + 8z + 10.

Practice Problems

Q 1. Find the value of the formula 9y - 2x if x = 5 and y = 3. (Ans: 17)

Q 2. For x = 8, what does the expression 9x - 1 represent? (Ans: 71)

Q 3. Find the value of the formula 5y - 2x if x = 2 and y = 1. (Ans: 1)

Summary

In simple mathematics, input refers to anything that enters a function. At the same time, the output is something the function generates. Functions and the ideas of input and output are connected in mathematics. You may also describe inputs and outputs as items you put into, use, operate, create, furnish, or provide. In this article, we have added the practice problem questions, so after going through the article, go through the practice problems to have more clarity over the topic.