




How to Find All Factors and Prime Factors of 39
In this article, we will learn how to compute the Factors of 39, their Prime factors, and their factors in pairs. We will also solve problems to help us to understand the topic. The integers, which are neither fractions nor decimals, are known as factors of 39. When multiplied in pairs, the numbers that provide the original number 39 are known as 39's factors. The pair factors of 39 might have both positive and negative values. The pair factors of 39. For example, it might be \[(1,39)\] or \[(-1,\text{ }-39)\]. When two negative numbers, \[-1\] and \[-39\] are multiplied, then the answer is 39.
What are the Factors of 39?
A factor of an integer is another integer that can divide the integer without leaving any remainder. There are 4 factors in 39. Factors of 39 are the numbers that divide 39 exactly with no remainder. Since the number 39 is an odd composite. So, it has more than two factors. As a result, the factors of 39 are 1, 3, 13, and 39.
How to Determine the Factors of 39?
The two steps help us to find 39's factors. As follows:
Step 1: Write the number 39, which has to be factored in.
Step 2: Find the two numbers whose product is 39.
Consider the integers 3 and 13 to be the two factors. In this case, 3 and 13 are prime numbers that cannot be divided further.
Both integers are now prime numbers.
So, 39 is expressed as the product of \[3\times 13=39\].
Thus, the factors of 39 are 1,3, 13, and 39.
Factors of 39 by Prime Factorisation
39 is a composite number that should have prime factors. Prime factorization of 39 refers to the method of determining the prime factors of 39. Divide 39 by the smallest prime number possible to get the prime factor of 39. Then, take the result and divide it by the lowest prime number. Repeat this step until you have 1.
Step 1: Divide 39 by 3.
\[39\div 3=13\]
Step 3: 13 is a prime number. So, divide 13 by 13.
\[13\div 13=1\]
Thus, we get 1 at the end of this division method, and we can’t go on with the division approach. Hence, the prime factorization of 39 is \[3\times 13\], where 3 and 13 are prime numbers. A number and a counting number are known as a multiple of the original number. So, the multiples of 39 are 39, 78, 117, 156, …
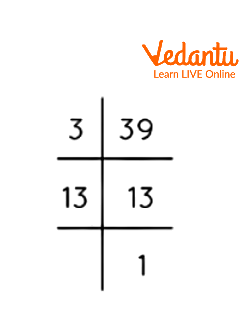
Prime Factorization of 39.
Factor Tree of 39
Factor trees represent the factors of a number, especially its prime factorization. Each tree branch is divided into factors. The end of the branch in the factor tree must be a prime number because the only two factors are itself and one, so the branch stops. We know that the prime factor of 39 is \[3\times 13\], where 3 and 13 are prime numbers. See its prime factor tree below.
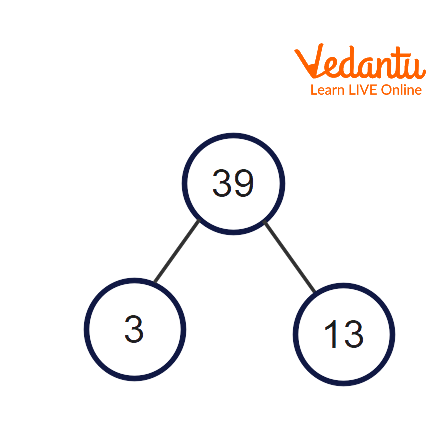
Factor Tree of 39
Factors of 39 in Pairs
The pair factors of 39 might have both positive and negative values. The pair factors of 39, for instance, might be \[(1,\text{ }39)\] or \[(-1,\text{ }-39)\]. When two negative numbers are multiplied, such as when \[-1\] and \[-39\] are multiplied, the answer is 39.
Pair factors of 39 are as follows:
Thus, the positive pair factors are \[(1,\text{ }39)\] and \[(3,\text{ }13)\].
Thus, the negative pair factors are \[(-1,\text{ }-39)\] and \[(-3,\text{ }-13)\].
Interesting Facts
We know that 39 is a composite number as it has more than two factors
Every number has the smallest factor, which is 1
Solved Important Questions
1. What are the factors of 39?
Ans: The integers that multiply to form the number 39 are known as the factors of 39.
\[1\times 39=39\]
\[3\times 13=39\]
So, the factors of 39 are 1, 3, 13 39.
2. Draw a factor tree of 69.
We know that the prime factorization of 69 is \[3\times 23\], where 3 and 23 are prime numbers. See its prime factor tree below.
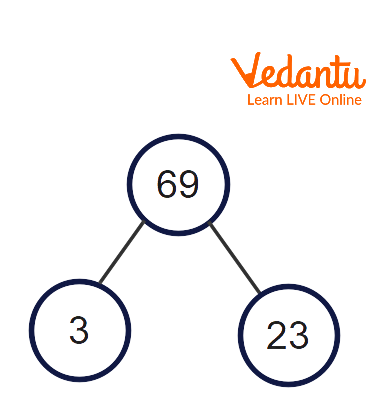
Factor Tree of 69
3. Draw a factor tree of 49.
Ans: Factor trees represent the factors of a number, especially its prime factorization. Each tree branch is divided into factors. The end of the branch in the factor tree must be a prime number because the only two factors are itself and one, so the branch stops. We should also remember that 1 is not a prime number; thus, it will not appear in any factor tree. We know that the prime factorization of 49 is \[7\times 7\], where 7 is a prime number.
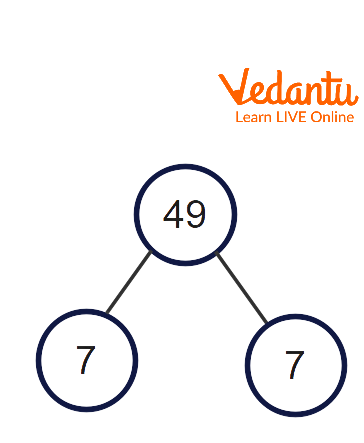
Factor Tree of 49
Practice Questions
1. What is the HCF of 39 and 69?
2
3
13
1
2. What is the sum of the factors of 39?
39
66
56
76
Answers:
Option B
Option C
Conclusion
The method for obtaining the 39 factors is explained in the article. The division method and the prime factorization method are two simple yet important methods that may be used to determine these factors. Factors of 39 are the integers that completely divide it without leaving any remainder. It has a total of 4 factors. Hence, the number 39 is composite, it has many factors other than 1 and 39. As a result, all the factors of 39 are 1, 3, 13 39 and the prime factorization of 39 is \[3\times 13\], where 3 and 13 are prime numbers.
FAQs on What Are the Factors of 39?
1. Find out the prime factors 250.
The term “prime factorization” refers to the process of expressing a composite number as the sum of its prime factors. The first step is to divide 250 by the lowest prime integer, which is 2.
\[250\div 2=125\]
Divide 125 by 5 because 125 is multiples of 5.
\[125\div 5=25\]
Again divide 25 by 5
\[25\div 5=5\]
Divide 5 by 5
\[5\div 5=1\]
Thus, the prime factorization of 250 is \[2\times 5\times 5\times 5\] or \[2\times {{5}^{3}}\], where 2 and 5 are prime numbers.
2. Find out the common factors of 39 and 69.
The numbers that divide the number exactly with no remainder are known as the factors of a number. So, the factors 39 and 69 are 1, 3, 13, 39, and 1, 3, 23, and 69 respectively.
Hence, the common factors of 39 and 69 are 1 and 3.
3. Find out the pair factors of 9.
Pair factors may be positive or negative, but they cannot be a fraction or a decimal. To get the pair factor of 9, multiply the two numbers in a pair to obtain the original number, which is 9, as follows:
Positive pair factors of 9:
\[\left( 1,9 \right)\] is a pair factor of 9 as \[1\times 9\]
\[\left( 3,3 \right)\] is a pair factor of 9 as \[3\times 3\]
Negative Pair Factors of 9:
\[\left( -1,\text{ }-9 \right)\] is a pair factor of 9 as \[-1\times -9\]
\[\left( -3,\text{ }-3 \right)\] is a pair factor of 9 as \[-3\times -3\]

















