Understanding the Division Statement in Maths

Here in this topic, we are going to learn to solve simple division problems. Dividing can be understood by distribution. In simple words, division means breaking large numbers into small numbers of equal parts. In other words, it can be understood by finding how many times a number is of another number. After studying this topic you will be able to know about basic division problems and how to solve a division problem. Let us get deeper into the pool of big numbers and break the numbers into smaller ones.

Parts of the Division Statement

The division has four parts. The first part is the number that is to be divided. This number is called Dividend. The second part is the number which will divide the dividend is called the divisor. The third part is the main answer which we will get by dividing the number. It is called a quotient. And the fourth part is called a remainder, which we get if the divisor can not divide the dividend completely.

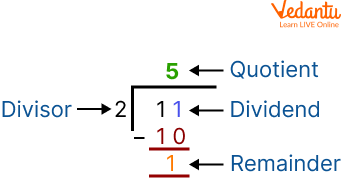
Parts of the division statement

Here in the image, 11 is the number that is to be divided so it is a dividend. 2 is the number that will divide the dividend 11, so it is the divisor. The main answer is the quotient. Here 5 is the quotient and the divisor could not divide the dividend completely, so here remainder is 1. A detailed explanation will be given later. In this section, just the name of parts of the division are given.

Formula of Division

To divide a number you have to remember a simple formula which is given below.

Formula of division

How to Solve a Division Problem?

Now we know the basic terminology of division and the formula of division. Now we will understand how to solve a division problem. For this, we will have to see how many times the divisor is of the dividend. In other languages, you just need to recall the table of divisors till you get the dividend or value less than it. Its value should not be greater than the dividend. Now you minus the dividend and the value you get. If the value after subtraction is 0, this means the divisor could divide the dividend completely. Otherwise, you have to repeat the process until the remainder is less than the divisor.

Division process

Properties of Division

There are mainly 4 properties of division, which are given below :

• When zero is divided by a number the quotient is zero.

Example: $0 \div 5=0$

• If we divide any number by one, the quotient is the number itself.

Example: $7 \div 1=7$

• If we divide a non zero number by itself, the quotient is one.

Example: $8+8=1$

• Division of a number by zero is not possible.

Solved Basic Division Problems

Q 1: Divide 8 by 4.

Ans. We have 8 as a dividend and 4 as a divisor. To solve this first we will have to make sure that the divisor should be less than the dividend. If this is the case next we will have to recall the table of 4 till we get 8. So 2 times 4 is 8. So here the answer that is quotient will be 2. And because the divisor that is 4 could divide the dividend that is 8 completely so the remainder will be 0.

Thus the quotient and remainder of the basic division problem are 2 and 0 respectively.

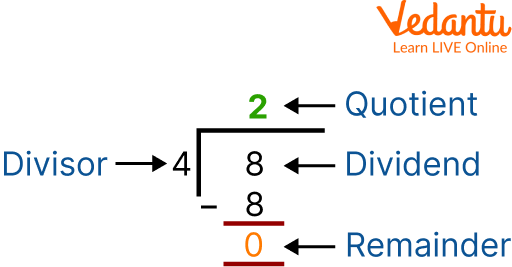
Basic division problem

Example 2: Divide 140 by 6.

Ans. As we can see the dividend is a large number in comparison to the previous example. We will take one value at a time for the dividend to be divided. We will take 1. We can see that 1 is smaller than 6.

But we have seen earlier that the divisor should be smaller than the dividend. So we will take the next digit of the dividend with it. In this way, we get 14, which is larger than 6. So we will recall the table of 6 till we get 14 or some number less than it, but it should not be greater than 14. So it will be 2 times 6.

Now we are subtracting 14 - 12, it will be 2 and 0 will now be get together with it. So, now $6 \div 20$.

So, if 6 multiplied by 3 we get 18, so now again on solvinhg it. We get 2 as remainder in the end. And now it can’t be divided anymore.

Thus the quotient and remainder of the basic division problem are 23 and 2 respectively.

Division of 140 by 6

Simple Division Problems for Practice

Q 1. Evaluate $625 \div 5$.

Ans. 125

Q 2. Solve $999 \div 9$.

Ans. 111

Q 3. What is $96 \div 6$?

Ans. 16

Summary

Now we know that division is the distribution of equal parts. To some extent division is related to multiplication, as division is the opposite of multiplication. In this article, we have learned how to solve division problems by understanding the concept of division statements, simple division problems, and basic division problems. You need to just practice as much as you can. We have studied the basic division problems with examples for solving them in detail. If you have any doubts you just need to read the “detailed explanation” of the division again to get a better understanding. Now you are ready to break the big numbers into small numbers in equal parts.