Divide Sums Questions for Kids
Understanding Division – Types, Examples, and Methods
Do you know what division is? Let us explain it to you in a simple manner. Suppose we give you six oranges and ask you to share them with two of your friends. But you must make sure that all three of you are having an equal number of oranges. So, what will you do? How will you divide them equally? Let us show you how.
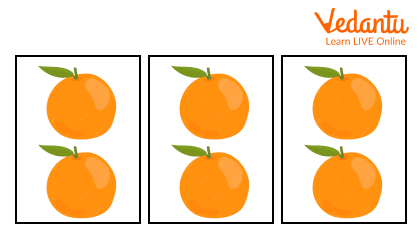
You have six oranges with you and you are three in total. In order to have equal numbers of oranges, you will have to divide six oranges into three equal parts. So what is 6 divided by 3? The answer is 2. Therefore, all three of you get 2 oranges each. Wasn’t that easy? So, this is what division is all about.
Meaning of Divide
In simple language, we can define divide or division as the separation of any number or things into two or more equal parts, groups, or categories. We can say that division is done to distribute any object or thing equally into many parts. In simple words, the meaning of divide is to distribute the whole thing to a group in equal parts.
For example, if we add a diagonal in a square, it will divide the square into two equal triangles which will also have equal areas. When two numbers are divided, the result can be either an integer, i.e., 2, 4, 6, 11, 12, or any number. It can also be a decimal, i.e., 3.34, 0.6, 1.5, or any other decimal number.
Symbol for Divide or Division
Divide or division can be easily represented using the division symbol (÷) or a slash (/) or even by using a horizontal line ( _ ). Also, if you are wondering how to pronounce it, then a/b or a÷b is read as ‘a by b’ or even ‘a over b’ or ‘a divided by b’.
For example, the division of 48 by 6 can be written as:
48 ÷ 6 = 8
48/6 = 8
486 = 8
Thus, all the three representations show the similar results.
Formula for Divide Sum
Before starting with the formula for division, we must keep in mind these four important terms – dividend, divisor, quotient, and remainder.
A number can be easily divided using the following formula:
Dividend = Divisor ✕ Quotient + Remainder
Now let us learn the meaning of each of the terms mentioned above.
The dividend represents the number which is to be divided and divisor is the number which is used to divide the dividend into equal parts.
Now, the result of this division is termed as a quotient and the left over number which is not divisible by the divisor is termed as remainder.
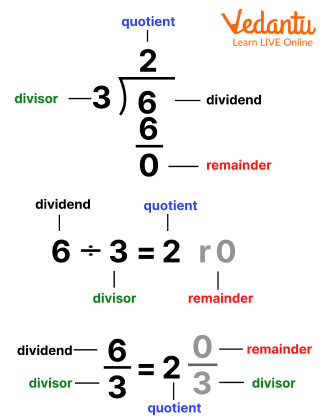
From the above image, we can see that 6 is the dividend which is to be divided by the divisor 3. We get 2 as the quotient and the remainder here is 0.
Rule for Division
The division rule includes four important steps which are mentioned below:
Firstly, we need to identify the dividend and the divisor. After identifying, we need to write them in their respective places.
Now, we will have to multiply the divisor with a number so that the result is closely similar to the dividend.
Subtract the result from the dividend in the dividend column.
Now, if the remaining value after subtraction is greater than the divisor, then continue the process again (as mentioned in step 2). Repeat the step until the remainder is less than the divisor.
For better understanding, refer to the image given below.
From the above image, we can see that the dividend is 359 and the divisor is 6. For easy calculation, let us first take the first part of the dividend, i.e., 35. Now, which number is closest to 35 and is divisible by 6? Let's start with remembering the multiplication table of 6. The number 30 is closest to 35. So, we will multiply 6 with 5 (as shown in the image).
Now, the subtraction result of 359 and 30 is 59, which is greater than divisor 6. So, we will repeat the step again, i.e., multiply 6 with 9 so that we get the number 54, which is closest to 59. We get the remainder as 5 which is smaller than the divisor 6, and hence, the division process is completed.
Special Cases of Division
Now that you have learned the rule and formula of division, you must also know about some special cases of division. There are mainly three special cases of division:
Case 1: When the divisor is 1
When the divisor is 1 or any number has to be divided by 1, the result will always be equal to the given number, i.e., the dividend.
For examples: 20÷ 1 = 20
3.5 ÷ 1 = 3.5
⅓ ÷ 1 = ⅓
Case 2 : When the divisor is 0
Since a number cannot be divided by 0, hence, the result will always be undefined.
Case 3: When the dividend is equal to the divisor
If both the dividend and the divisor have the same value, then the answer will always be equal to 1.
For example: 20 ÷ 20 = 1
3.5 ÷ 3.5 = 1
⅓ ÷ ⅓ = 1
Great! Now you have learnt all the important formulas and rules of division. Wasn’t it easy and fun? Hope this article helped you in clearing your concept on division. You can also find many more solved problems on division at our website. Do check them out and practise regularly to score good marks on this topic.
FAQs on Divide Sums
1. Define the long division method in Mathematics.
The long division method in Mathematics is used to divide large numbers into equal groups or parts. This method helps in dividing a sum into a series of easier steps. The long division method is similar to other division methods where the dividend is divided by the divisor to give a result called the quotient and sometimes a remainder.
2. What is the difference between a divisor and a factor?
Any number that divides the dividend leaving a quotient and a remainder is called a divisor. A factor, on the other hand, is a divisor that completely divides the number and leaves no remainder. As a result, all factors of a number are its divisors. But not all divisors will be factors.
