Introduction
Cross Multiplication is generally used for calculations of fractions for equating unequal denominators and simplifying them and solving the required operations. Using the same steps, a cross multiplication formula was derived which can be used to solve the linear equations in two variables easily and efficiently.
What is an Equation?
We all are very familiar with the term equations, which in general refers to two math based expressions which are connected by an equal sign.
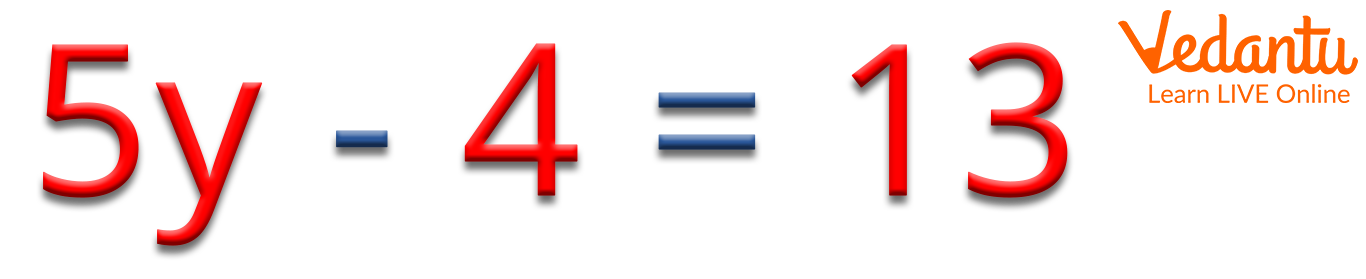
Example of an Equation
Here, in the above image the expression \[5{\rm{y}} - 4 = 13\]
, 5 is the coefficient of the variable y and 4 is the constant.
Constant : In simple words, the numerical value which does not change or in simple terms, it does not have an alphabet i.e. variable with it is termed as a constant.
Variable : The term whose value varies and may be not known and is generally denoted by the english alphabet is a variable.
Coefficient : The number which is accompanied by a variable is termed as the coefficient of that variable. If there is no coefficient to the variable it is considered to be one.
What is a Linear Equation?
As we all are well versed with the terms constant and variables, the equation in which the highest power of the variable is 1 is termed as a linear equation.
What is a Linear Equation in Two Variables ?
A linear equation which has two variables whose highest power is 1 is said to be a linear equation in two variables.
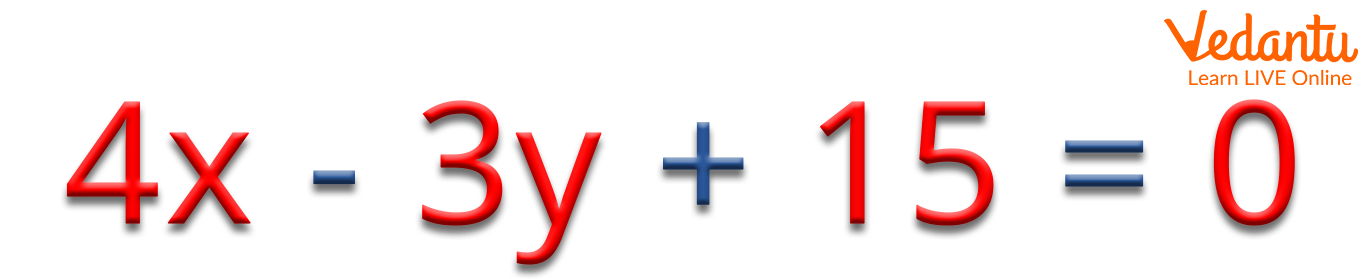
Example of a Linear Equation in Two Variables
Methods for Solving Simultaneous Linear Equations :
Generally, there are three methods for solving two simultaneous linear equations - Substitution method, Elimination method and Cross- Multiplication method.
What is the Cross Multiplication Method ?
Cross multiplication method is the easiest method of solving simultaneous linear equations and it can be used only when there are two linear equations in two variables. In cross multiplication, we generally multiply the numerator of the first fraction with the denominator of the second and numerator of second with the denominator of first. Here, to understand the formula we use the following two equations :
\[{{\rm{a}}_{\rm{1}}}{\rm{x}} + {{\rm{b}}_{\rm{1}}}{\rm{y}} + {{\rm{c}}_1} = 0\]
\[{{\rm{a}}_{\rm{2}}}{\rm{x}} + {{\rm{b}}_{\rm{2}}}{\rm{y}} + {{\rm{c}}_2} = 0\]
Here, we can see that \[{{\rm{a}}_{\rm{1}}}\] and \[{{\rm{a}}_{\rm{2}}}\] are the coefficients of x ; \[{{\rm{b}}_{\rm{1}}}\]and \[{{\rm{b}}_{\rm{2}}}\] are the coefficients of y and \[{{\rm{c}}_{\rm{1}}}\] and \[{{\rm{c}}_{\rm{2}}}\]are the constants.
So, we can find the values of x and y by cross multiplication formula by using the steps given in the following image :
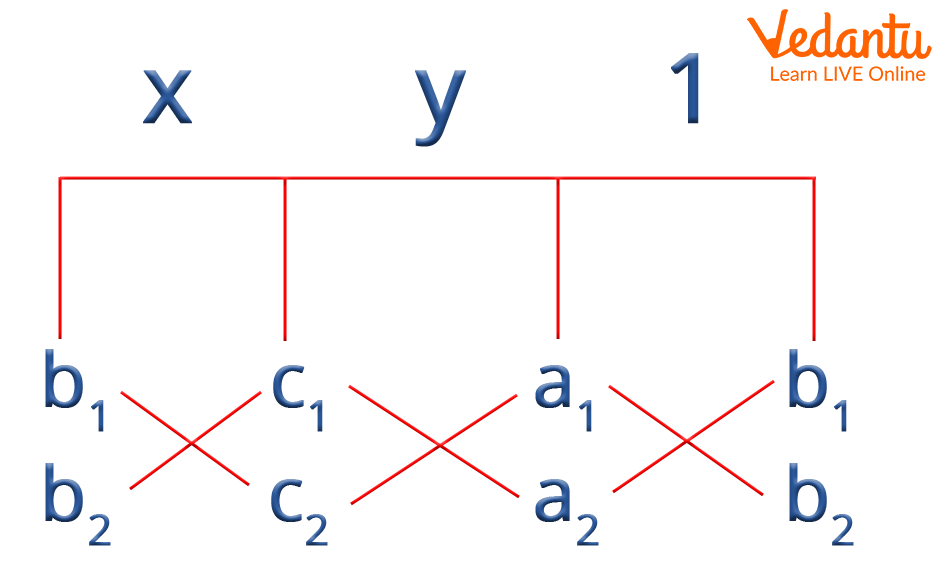
Cross-Multiplication formula
From the above image, we get the relation :
\[\frac{{\rm{x}}}{{{{\rm{b}}_{\rm{1}}}{{\rm{c}}_{\rm{2}}} - {{\rm{b}}_{\rm{2}}}{{\rm{c}}_{\rm{1}}}}} = \frac{{\rm{y}}}{{{{\rm{c}}_{\rm{1}}}{{\rm{a}}_{\rm{2}}} - {{\rm{c}}_{\rm{2}}}{{\rm{a}}_1}}} = \frac{1}{{{{\rm{a}}_{\rm{1}}}{{\rm{b}}_{\rm{2}}} - {{\rm{a}}_{\rm{2}}}{{\rm{b}}_{\rm{1}}}}}\]
On simplifying the the relation we can get the values of x and y
Solved Examples :
Solve the given pair of linear equations using the cross multiplication formula :
\[7{\rm{x}} + 3{\rm{y + 4 = 0}}\]
\[4{\rm{x + y + 2 = 0}}\]
Solution : Here, 7 and 4 are the coefficients of x ; 3 and 1 are the coefficients of y and 4 and 2 are the constants.
Now, using the cross multiplication formula we have :
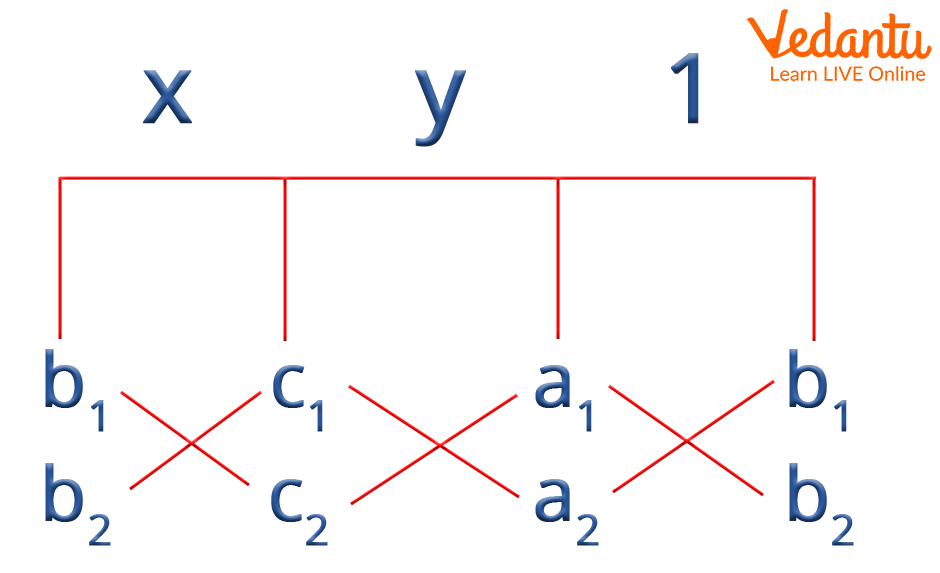
Cross Multiplication Formula
\[\frac{{\rm{x}}}{{{{\rm{b}}_{\rm{1}}}{{\rm{c}}_{\rm{2}}} - {{\rm{b}}_{\rm{2}}}{{\rm{c}}_{\rm{1}}}}} = \frac{{\rm{y}}}{{{{\rm{c}}_{\rm{1}}}{{\rm{a}}_{\rm{2}}} - {{\rm{c}}_{\rm{2}}}{{\rm{a}}_1}}} = \frac{1}{{{{\rm{a}}_{\rm{1}}}{{\rm{b}}_{\rm{2}}} - {{\rm{a}}_{\rm{2}}}{{\rm{b}}_{\rm{1}}}}}\]
Using the above result , we have :
\[\frac{{\rm{x}}}{{3 \times 2 - 1 \times 4}} = \frac{{\rm{y}}}{{4 \times 4 - 2 \times 7}} = \frac{1}{{7 \times 1 - 4 \times 3}}\]
\[\frac{{\rm{x}}}{{6 - 4}} = \frac{{\rm{y}}}{{16 - 14}} = \frac{1}{{7 - 12}}\]
\[\frac{{\rm{x}}}{2} = \frac{{\rm{y}}}{2} = \frac{1}{{ - 5}}\]
On equating x with the constant term,
\[x = - \frac{2}{5}\]
On equating y with the constant term,
\[{\rm{y}} = - \frac{2}{5}\]
Solve the given pair of linear equations using the cross multiplication formula :
\[{\rm{x}} + {\rm{y}} - 8 = 0\]
\[5{\rm{x}} + 3{\rm{y}} + 2 = 0\]
Solution : Here, 1 and 5 are the coefficients of x ; 1 and 3 are the coefficients of y and -8 and 2 are the constants. Now, using the cross multiplication formula we have :
\[\frac{{\rm{x}}}{{{{\rm{b}}_{\rm{1}}}{{\rm{c}}_{\rm{2}}} - {{\rm{b}}_{\rm{2}}}{{\rm{c}}_{\rm{1}}}}} = \frac{{\rm{y}}}{{{{\rm{c}}_{\rm{1}}}{{\rm{a}}_{\rm{2}}} - {{\rm{c}}_{\rm{2}}}{{\rm{a}}_1}}} = \frac{1}{{{{\rm{a}}_{\rm{1}}}{{\rm{b}}_{\rm{2}}} - {{\rm{a}}_{\rm{2}}}{{\rm{b}}_{\rm{1}}}}}\]
Using the above result , we have :
\[\frac{{\rm{x}}}{{1 \times 2 - 3 \times [ - 8]}} = \frac{{\rm{y}}}{{[ - 8] \times 5 - 2 \times 1}} = \frac{1}{{1 \times 3 - 5 \times 1}}\]
\[\frac{{\rm{x}}}{{2 - [ - 24]}} = \frac{{\rm{y}}}{{ - 40 - 2}} = \frac{1}{{3 - 5}}\]
\[\frac{{\rm{x}}}{{26}} = \frac{{\rm{y}}}{{ - 42}} = \frac{1}{{ - 2}}\]
On equating x with the constant term,
\[x = - \frac{{26}}{2} = - 13\]
On equating y with the constant term,
\[{\rm{y}} = \frac{{ - 42}}{{ - 2}} = 21\]
Solve the given pair of linear equations using the cross multiplication formula :
\[4{\rm{x}} + 2{\rm{y}} + 3 = 0\]
\[3{\rm{x}} - 7{\rm{y}} - 2 = 0\]
Solution : Here, 4 and 3 are the coefficients of x ; 2 and -7 are the coefficients of y and 3 and -2 are the constants.
Now, using the cross multiplication formula we have :
\[\frac{{\rm{x}}}{{{{\rm{b}}_{\rm{1}}}{{\rm{c}}_{\rm{2}}} - {{\rm{b}}_{\rm{2}}}{{\rm{c}}_{\rm{1}}}}} = \frac{{\rm{y}}}{{{{\rm{c}}_{\rm{1}}}{{\rm{a}}_{\rm{2}}} - {{\rm{c}}_{\rm{2}}}{{\rm{a}}_1}}} = \frac{1}{{{{\rm{a}}_{\rm{1}}}{{\rm{b}}_{\rm{2}}} - {{\rm{a}}_{\rm{2}}}{{\rm{b}}_{\rm{1}}}}}\]
Using the above result , we have :
\[\frac{{\rm{x}}}{{2 \times [ - 2] - [ - 7] \times 3}} = \frac{{\rm{y}}}{{3 \times 3 - [ - 2] \times 4}} = \frac{1}{{4 \times [ - 7] - 3 \times 2}}\]
\[\frac{{\rm{x}}}{{ - 4 - [ - 21]}} = \frac{{\rm{y}}}{{9 - [ - 8]}} = \frac{1}{{ - 28 - 6}}\]
\[\frac{{\rm{x}}}{{17}} = \frac{{\rm{y}}}{{17}} = \frac{1}{{34}}\]
On equating x with the constant term,
\[{\rm{x}} = \frac{{17}}{{34}} = \frac{1}{2}\]
On equating y with the constant term,
\[{\rm{y}} = \frac{{17}}{{34}} = \frac{1}{2}\]
Conclusion:
Cross multiplication method is one of the three methods for solving pairs of linear equations in two variables and is the easiest one among them. In this we generally cross multiply the terms of the two equations and the formed result is generally used as a formula to solve the sums easily and efficiently. After substituting the values as per the question in the formula, we equate it to the constant term to find the values of x and y respectively.
FAQs on Method of Cross Multiplication
1.How do we find whether the pair of linear equations given form a pair of coincident lines?
We can do so by checking the following condition :
i.e. \[\frac{{{a_1}}}{{{a_2}}} = \frac{{{b_1}}}{{{b_2}}} = \frac{{{c_1}}}{{{c_2}}}\]
If the above condition is true, there exists infinitely many solutions and the pair of lines are thus coincident.
2.When do the pair of lines give a unique solution ?
When the proportion of the coefficient of the variables is not equal then the equations will have a unique solution.
\[\frac{{{\rm{a_1}}}}{{{\rm{a_2}}}} \ne\frac{{{\rm{b_1}}}}{{{\rm{b_2}}}}\]
i.e. \[\frac{{{\rm{a_1}}}}{{{\rm{a_2}}}} \ne \frac{{{\rm{b_1}}}}{{{\rm{b_2}}}}\]
3.When do the pair of lines have no solution ?
If the coefficient of variables follows the condition\[\frac{{{a_1}}}{{{a_2}}} = \frac{{{b_1}}}{{{b_2}}} \ne \frac{{{c_1}}}{{{c_2}}}\]
, the pair of linear equations will have no solution and are said to be inconsistent.
4.When will the pair of linear equations have infinitely many solutions?
When we write the ratios in terms of the cross multiplication formula, the denominators of the proportional ratios must be zero to have infinitely many solutions.
\[\frac{{{\rm{a_1}}}}{{{\rm{a_2}}}}=\frac{{{\rm{b_1}}}}{{{\rm{b_2}}}}=\frac{{{\rm{c_1}}}}{{{\rm{c_2}}}}\]
