Understanding the Associative Property of Multiplication

First, try calculating \[\left( 2\times 3 \right)\times 4\]. And then \[2\times \left( 3\times 4 \right)\]. Does it give you the same result?

If it has given you the same result, congratulations because multiplication does have the associative property and the result does not change even if you change the order of multiplying the numbers. The order of associating the factors does not influence the final product of the operation.

\[(a \times b) \times c=a \times(b \times c)=(a \times c) \times b\]

If \[a=4\], \[b=6\] and \[c=10\], we are left with:

\[4 \times 6 \times 10=24 \times 10=240\]

\[4\times \left( 6\times 10 \right)-4\times 60=240\]

\[\left( 4\times 10 \right)-\times 6= 4\times 6 = 240\]

Associative Property Example

Now let's see how this property is fulfilled with another more visual example:

Let's count the number of cubes in the following image. In total there are 24 cubes.

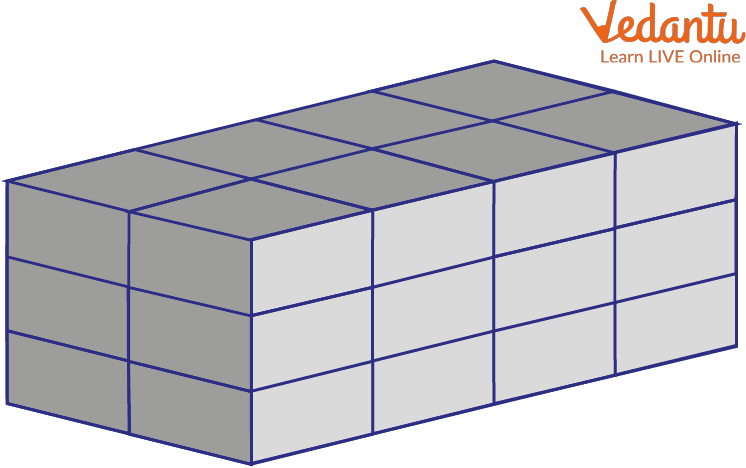
A Box of Cubes

Count the number of cubes, there are several ways to do it apart from counting one by one.

One way is to first count the cubes in a single column.

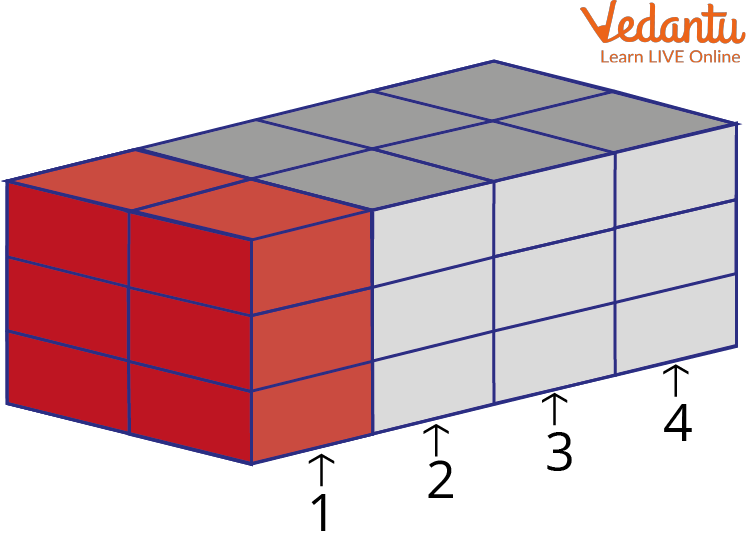
The Box with One Colored Column

If you look at the first orange-colored column there are \[3 \times 2=6,6\] cubes. How many columns are there in total? All right, there are \[4\] columns. So \[6\] times \[4\] gives us the total number of cubes there are, which is \[24\] cubes.

Another way is by counting the cubes in a row.

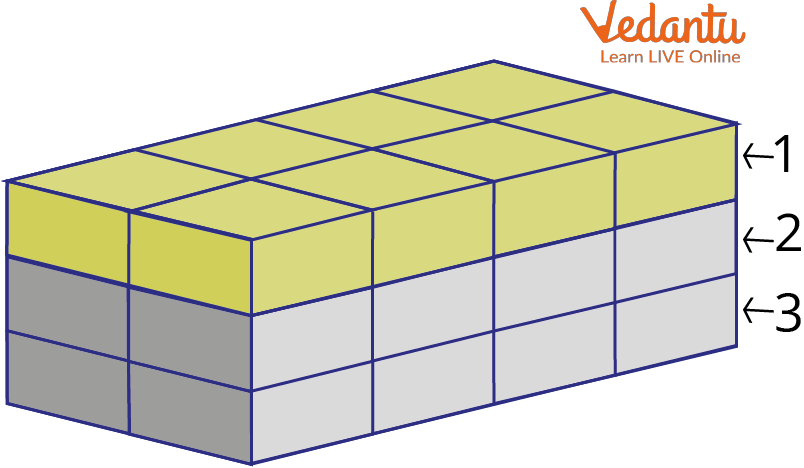
The Box with One Colored Row

In the first row colored green there are \[4 \times 2=8,8\] cubes. And since there are \[3\] rows in total, to calculate the total number of cubes there are, we make \[8 \times 3\], which is \[24\]. There are \[24\] cubes in total.

We have performed the following operations:

\[\left( 3\times 2 \right) \times 4 = 3 \times \left( 2\times 4 \right)\]

\[6 \times 4=3 \times 8\]

\[24=24\]

What is the Associative Property of Multiplication?

Regardless of how you group the factors, the result remains the same.

Multiplication is an operation that has several properties. One of them is the associative property. So, what is associative property? This property tells us that the way of grouping the factors does not alter the product of the multiplication, whatever the number of factors there are.

How easy is the associative property of multiplication, right?

How may the Associative Attribute be used to Solve a Problem?

The associative property states that no matter how we arrange the items with which we do addition or multiplication, the outcome will always be the same. Let's examine the associative property of multiplication in more detail.

The Associative Property of Multiplication

It doesn't matter how we combine the elements to multiply three or more integers because the result will always be the same.

The associative property formula for multiplicationcan be written as: \[\left( a\times b \right) \times c = a \times \left( b\times c \right)\]

Let's see an associative property example in a problem:

To bring new balls to a sports center, \[2\] trucks have arrived with \[10\] boxes each. Inside each box, there are \[8\] balls. How many balls have arrived at the sports center?

Although there are two ways we may organize the components to solve it, the outcome will always be the same \[(160)\]. Check it out in the subsequent images:

To determine the total number of boxes, multiply the trucks by the number of boxes each truck contains \[2 \times 10\]. Following that, we multiply by the number of balls in each box \[20 \times 8\], giving us a total of \[160\] ball s:

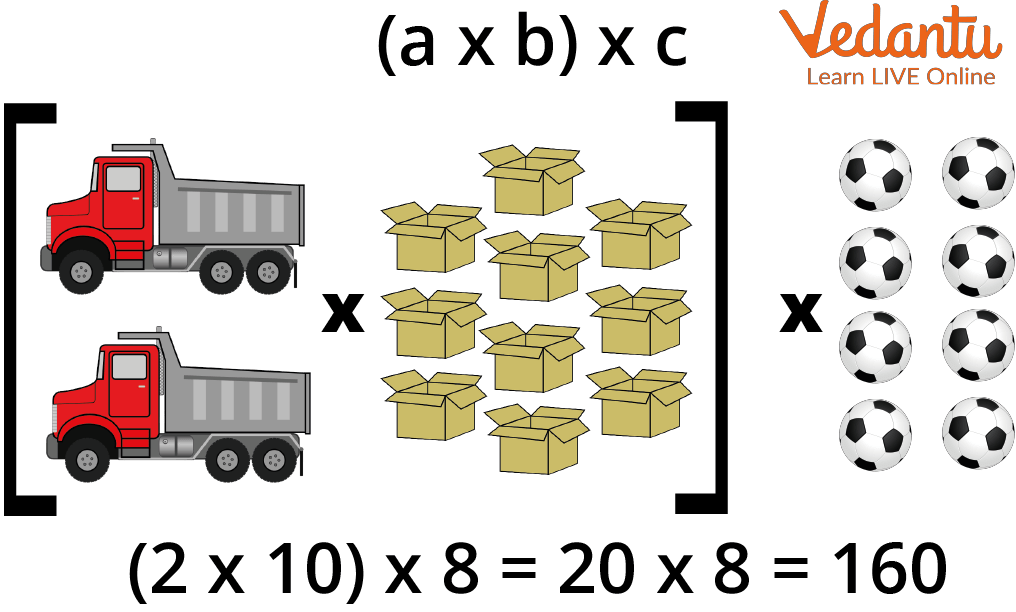
The LHS Solution of Associative Law of Multiplication

If we first multiply the boxes by the number of balls in each box \[10 \times 8\], we will get the number of balls per truck. Then we multiply by the number of trucks \[80 \times 2\] and it will give us \[160\] balls in total:

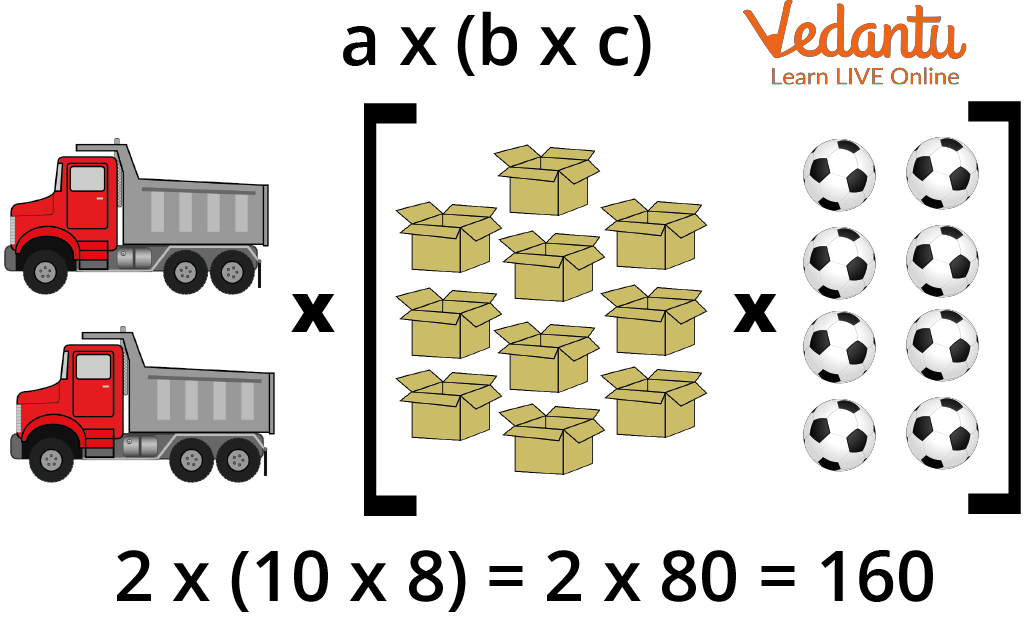
The RHS Solution of the Associative Law of Multiplication

Practice on your own

Q1: Which of the following expressions shows the associative law of multiplication and is equal to \[8 \times(3 \times 2)\]?

(a) \[(8 \times 3) \times 2\]

(b) \[(8+3) \times 2\]

Ans: (a) \[(8 \times 3) \times 2\]

Q2: Does this equation follow the associative property of multiplication?

\[(26 \times 3 \times 1) \times 4=26 \times(3 \times 1 \times 4)\]

Ans: Yes

Summary

Whenever you do a problem in which you have to multiply or add, remember that you can group its elements as you see fit. The associative property of multiplication says "The order in which the factors are grouped or associated does not alter the product." Therefore, for any real numbers \[a\], \[b\], and \[c,(a \times b) \times c=a \times(b \times c)\]. This property is helpful to know while solving maths problems, because it can sometimes make calculations simpler and less time-consuming. The next time you need to multiply numbers, remember the associative property formula and simplify your work by choosing the order that is easiest for you.