




How to Add Measurements Easily with Examples
We frequently wonder how tall some items are when we see their heights, like hills, towers, buildings, long trees, bridges, railways, etc. The height of something is commonly referred to as its length. For example, we often say the length of the railroad or the bridge. The dimension of distance for length is a feature of the International System of Quantities.
Different units can be used to add length. However, before adding length, we must check that the units of the two lengths are similar; if not, we must first convert them to similar units before adding them.

Length
What is Length Measurement?
A measurement is the length of an object in a certain unit. Understanding and measuring the lengths of objects is an essential skill since it allows us to interact more properly with our surrounding environment.
Length Unit
The length of something used as a measurement for an object. The metre, written as m, serves as the fundamental unit of length in the International System of Units (SI) system. This is possible when the length is given in the proper measurements, such as 5 metres or 500 centimetres for a box and 60 metres for a rope. As a result, the units of measurement are used to understand the supplied parameters in number format.
Table of Length Conversion
Worksheet on Addition of Length
Let’s have a look at the addition of length worksheet:
Example 1: Add 20m and 65m.
Solution: Lengths can be directly added as both have the same units.
On adding 20m and 65m,

20+65
Therefore, on adding 20m and 65m, we get 85m.
Example 2: Add 60 m, 25 cm and 8 cm.
Solution: Lengths cannot be directly added as the units are different. So, we will have to convert m to cm to perform addition.
On converting 60 m,
$ = \left( {60 \times 100} \right)cm = 6000 cm$ [1m = 100cm]
Then, the addition of all these values after conversion is given by,

6000 + 25 + 8
Therefore, on adding 60 m, 25 cm and 8 cm, we get 6,033cm.
Example 3: Subtract 10 km and 100 km.
Solution: Lengths can be directly subtracted as both have the same units.
On subtracting 10 km and 100 km,

100 - 10
Therefore, on subtracting 100 km and 10km, we get 90 km.
Example 4: Add 21 mm and 200 cm.
Solution: Lengths can be directly added as both have the same units. So, we will have to convert cm to mm in order to perform addition.
On converting 200 cm,
$ = \left( {200 \times 10} \right)mm = 2000mm$ [1cm = 100mm]
Then, the addition of all these values after conversion is given,

2000+21
Therefore, on adding 21 mm and 200 cm, we get 2,021cm.
Example 5: Subtract 99 cm and 20cm.
Solution: Lengths can be directly subtracted as both have the same units.
On subtracting 99 mm and 20mm,
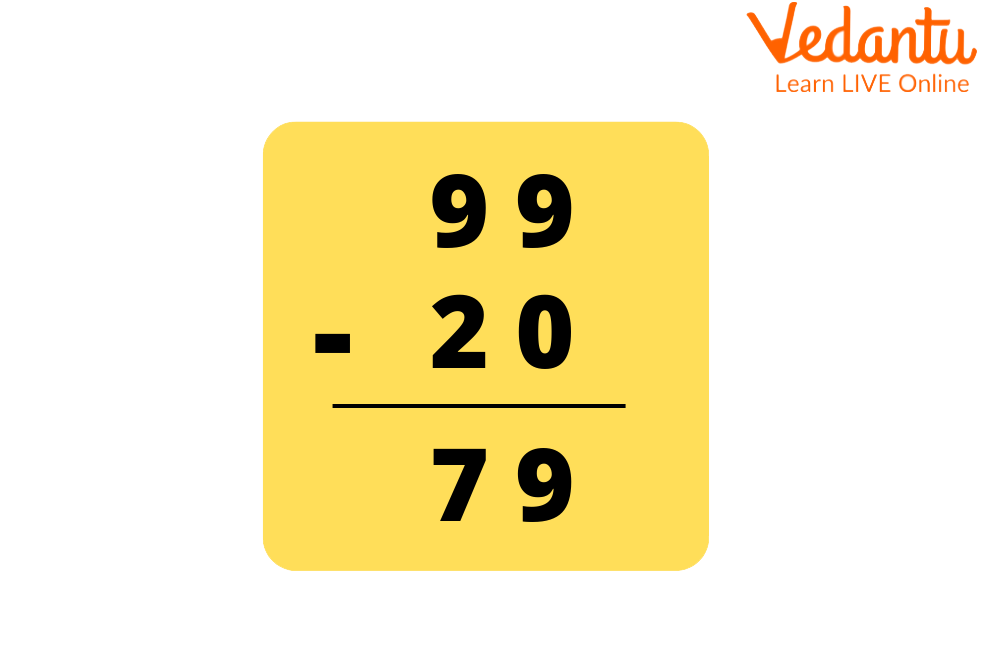
99 - 20
Therefore, on subtracting 99 cm and 20cm, we get 79cm.
Example 6: Add 109 cm and 90 cm.
Solution: Lengths can be directly added as both have the same units.
On adding 109 cm and 90cm,

109 + 90
Therefore, on adding 109 cm and 90 cm, we get 199 cm.
Conclusion:
The height of something is frequently referred to as its length. When something is described as being long, it means it is long when measured end to end. Calculating an object's length in a certain unit is called length measuring. For instance, the table above reveals the length of a ruler. So, in this article, we have learned about the length, its SI unit and the basic conversion of length.
FAQs on Addition of Length Explained: Step-by-Step Guide
1. What are measurement advantages?
Measuring is important in many other fields and activities than science and the chemical industry, such as farming, engineering, construction, manufacturing, and business.
2. What is a primary length unit?
The metre is the primary unit of length in the metric system. The metre is the basis for all length units in the metric system.
3. What measurement of length is used?
The inch, foot, yard, and mile are the fundamental units of length and distance measurement in the English system. The rod, furlong, and chain are additional length units. Areas are commonly expressed in square feet or square yards.























