Adding and Subtracting Fractions Made Easy

Adding and subtracting fractions is a common maths problem every student has to solve at some point in their lives. Fractions are an excellent way to represent numbers and can be applied in various contexts. When you multiply like fractions together, the result is always a fraction.

With denominators, fractions can be added and subtracted. The process of adding and subtracting is done by checking the denominator. This section will discuss adding and subtracting fractions with denominators, one of the students’ most common problems. In addition to solving this problem, we will also discuss how to add or subtract fractions with denominators.

Addition of Fraction

How Do You Add or Subtract Fractions?

Fraction addition and subtraction follow similar rules, with the denominators checked before the addition or subtraction begins. After we have checked the denominators, we can add or subtract the specified fractions.

The denominators are examined in the following manner:

1. Numerators are added or subtracted if the denominators of the fractions are the same.

2. If the denominators differ, we convert the fractions to like fractions so that the denominators match, and then we add or subtract as needed.

Example: $\dfrac{1}{7}+\dfrac{4}{7}=\dfrac{5}{7}$

$\dfrac{4}{5}-\dfrac{1}{5}=\dfrac{3}{5}$

Adding and Subtracting Fractions with Like Denominators

As we just need to work with the numerators, adding and subtracting fractions with like denominators is fairly simple. Here, we just need to add the numerator, while keeping the same denominator.

How Do You Add Fractions with the Same Denominators?

The following are steps to be taken care of while adding fractions with the same or like denominator:

Step 1: First, we must add the numerators of the given fraction.

Step 2: Since the denominator is the same. So we will keep it.

Step 3: Now, just add the numerator.

$\dfrac{\mathrm{a}}{\mathrm{b}}+\dfrac{\mathrm{c}}{\mathrm{b}}=\dfrac{\mathrm{a}+\mathrm{c}}{\mathrm{b}}$

Note: For Subtractions also, the method is the same.

In this case, we need to subtract $\dfrac{2}{5} - \dfrac{1}{5}$. Let us understand the procedure using the following steps.

Step 1: We will subtract the numerators of the given fractions. Here, the numerators are 2 and 1, so it will be 2 - 1 = 1

Step 2: Retain the same denominator. Here, the denominator is 5.

Step 3: Therefore, the difference of $\dfrac{2}{5} - \dfrac{1}{5}$

= $\dfrac{2 - 1}{5}$

= $\dfrac{1}{5}$

Adding and Subtracting Fractions with Like Denominators: Examples

Example: Add the fractions together.

$\dfrac{3}{7}+\dfrac{2}{7}$

Ans: Both of the fraction’s denominators are 7. These fractions are simple to add since they have the same denominator. To do so, simply add their numerators and retain their denominator, which is $7 .$

$\dfrac{3}{7}+\dfrac{2}{7} =\dfrac{3+2}{7}$

$=\dfrac{5}{7}$

Example: Add the fractions together.

$\dfrac{2}{11}+\dfrac{1}{11}+\dfrac{5}{11}$

Ans: Place the sum over the common denominator, 11, after adding the numerators.

$\dfrac{2}{11}+\dfrac{1}{11}+\dfrac{5}{11}=\dfrac{2+1+5}{11}=\dfrac{8}{11}$.

Example: Find the value of $\dfrac{4}{5}$ - $\dfrac{2}{5}$

Ans: Let's use a rectangle model to subtract the decimal fractions $\dfrac{4}{5}$ and $\dfrac{2}{5}$. This model indicates $\dfrac{4}{5}$ by darkening 4 of the 5 components. To simulate deleting $\dfrac{2}{5}$, we will further shade 2 portions from our shaded model.

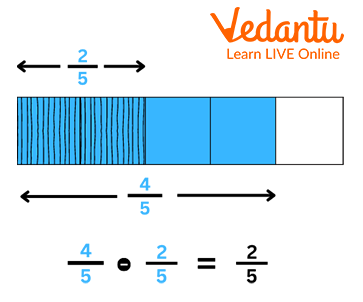
Subtraction of Fraction

Worksheet for Adding and Subtracting Fractions with Like Denominators

Here is a worksheet related to adding and subtracting fractions with denominators, which will be very useful for the students.

Q1. $\dfrac{5}{11}+\dfrac{4}{11}=$

Ans: $\dfrac{9}{11}$

Q2. $\dfrac{12}{20}-\dfrac{5}{20}=$

Ans: $\dfrac{7}{20}$

Q3. $\dfrac{12}{15}+\dfrac{9}{15}=$

Ans: $\dfrac{21}{15}$

Q4. $\dfrac{7}{15}-\dfrac{6}{15}=$

Ans: $\dfrac{1}{15}$

Q5. $\dfrac{7}{5}-\dfrac{4}{5}=$

Ans: $\dfrac{3}{5}$

Summary

This article taught us how to easily add or subtract fractions. What we have to do is just keep the denominator the same and add or subtract the numerator as per the requirement and then just solve it. In this way, we can easily add or subtract the like fractions. We have also added some solved examples and practice problems on adding and subtracting, like fractions. Through this, we can have more clarity on the topic. We hope this article will help you in getting command over the topic.