CBSE Physics Experiment To Find the Weight of a Given Body Using Parallelogram Law of Vectors

Utilizing the parallelogram's vector law can aid in developing an understanding of an object's weight as well as determining the direction of material flow. The Parallelogram law of vectors addition explains how the diagonal of a parallelogram can appear if vectors are displayed in the same direction.

According to the parallelogram law, the total of the squares representing the lengths of a parallelogram's four sides equals the total of the squares representing the lengths of its two diagonals. It is necessary for the parallelogram in Euclidean geometry to have equal opposite sides.

Table of Content

• Aim

• Overview of Parallelogram law of vector addition

• Diagram of parallelogram

• Apparatus Required

• Theory

• Procedure

• Results

Aim

Measurement of the weight of a given body (a wooden block) using the parallelogram law of vector addition.

Apparatus Required

• Gravesand’s Apparatus (a vertical wooden board with two pulleys)

• Three hangers

• A known object whose mass needs to be calculated

• Thin rope

• White sheets of paper

• A strip of mirrors

• Protector 

• Thumb pins

• Scale of one-half meter

• A spring balance

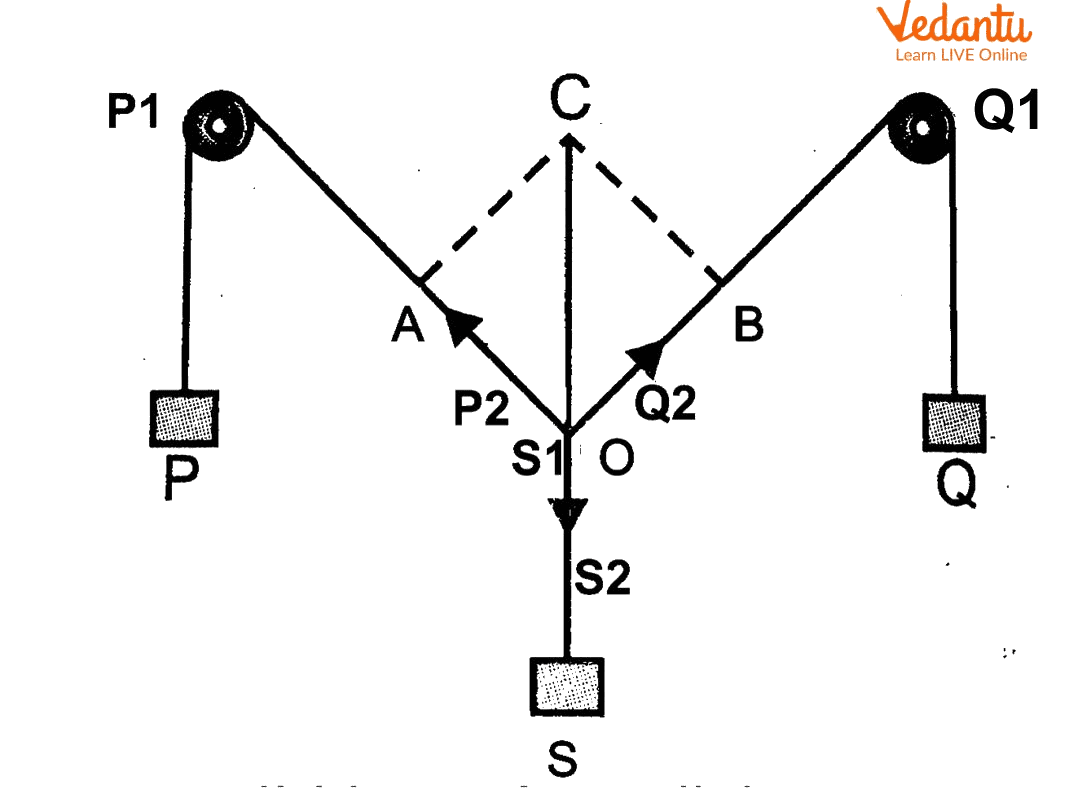
Diagram of Parallelogram Law of Vector Addition

Theory 

The forces acting on the object suspended in the middle are equal to the vector sum of the forces felt by the two masses hanging on the pulley. The middle mass also feels a similar force. When two balancing weights P and Q are slung from the hanger's other two ends and a body S with an unknown weight hanging from its center, the unknown weight is calculated as follows:

\[{\rm{S = }}\sqrt {\left( {{P^2} + {Q^2} + 2PQ{\rm{Cos}}\theta } \right)} \]

S stands for "unknown weight" in this context. P and Q are the balance weights.

Assuming a scale (let's say 1 cm=50 gwt) that corresponds to the weights P and Q, create the parallelogram OACB at this point. The diagonal vector is the rationale for the outcome and can be observed from the parallelogram. The size of the unidentified body,

\[{\rm{S = OC}} \times {\rm{Scale}}\]

The experiment's % error can be computed using the equation if W is the body's actual weight:

​​\[{\rm{Percentage}}\;{\rm{error = }}\dfrac{{{\rm{Actual~weight - Calculated~weight}}}}{{{\rm{Actual~weight}}}}{\rm{ \times 100}}\]

\[ = \dfrac{{W - S}}{W} \times 100\]

Procedure

1. Place the Gravesand device firmly and vertically on a table. Check to see that the pulleys are operating properly.

2. Using thumb pins, put a white piece of paper between the board's pulleys.

3. Put a thread over the pulley and tie the ends to the hooks of the hanger weights. You can suspend the unknown weight from this one by tying another thread in the middle of the string that passes over the pulleys. You can suspend the unknown weight from this one by tying another thread in the middle of the string that passes over pulleys.

4. The knot (of the two strings) should be in the centre of the sheet after you place a slotted weight on the hangers and adjust it.

5. Lay the plane mirror strip under each string one at a time to determine the direction of the forces. Mark the ends of the mirror strip by positioning your eye such that the string itself obscures the image of the string.

6. After removing the paper, connect each pair of points such that they all meet at O.

7. Mark the OA and OB sides using a convenient scale (for instance, if P = 150 g and Q = 150 g). OA = 3 cm, while OB = 3 cm. The OACB parallelogram is finished. Join the diagonal OCs, measure them, and then translate their weights into equivalent grams. This weight will be the same as the weight hung at S. Weigh the object with a spring balance for more assurance.

8. To repeat the experiment, adjust the weight in hangers P and Q two more times.

Observation Table

Spring balance Least Count: ……g

Spring balance zero error: …..g

Weight of unknown body using spring balance: …..g

The scale used: Let 1 cm = 50 g

Mean unknown weight, \[S = \dfrac{{\left( {S1 + S2 + S3} \right)}}{3}\]

Percentage error: _____.

Result

The weight of the given body is =  ____N

The error falls within the acceptable experimental error margin.

Precautions

1. The board should be in a steady and vertical posture.

2. It is forbidden for the hangers to touch the board or table marking should only be done when the weights are at rest.

3. Use an appropriate scale to construct a rather large parallelogram.

Lab Manual Questions

1. Given two forces, what could be the (a) Maximum angle of the resultant force. (b) Minimum angle of the resultant force.

Ans. The maximum angle of the resultant force is 0°.

The minimum angle of the resultant force is 180°

2. Why is vector addition different from scalar addition?

Ans: A vector addition contains direction and magnitude, whereas a scalar addition simply has magnitude. As a result, adding a vector is different from adding a scalar.

3. How will the parallelogram modify if all three forces are equal in magnitude?

Ans. When three equal forces are involved in the parallelogram, these are bent toward one another equally by 120°. These three forces are equal to the sum of the other two forces if the product of the three forces equals zero. 

4. State parallelogram law of vector addition.

Ans. According to the law of vector addition known as the parallelogram, when two vectors act simultaneously in both magnitude and direction by the adjacent sides of a parallelogram drawn from the same point, their resultant vector is represented both in magnitude and direction by the parallelogram's diagonal.

Viva Questions

1. What distinguishes vector addition from scalar addition?

Ans. Adding a vector adds magnitude and direction, whereas adding a scalar only adds magnitude. Therefore, adding a vector differs from adding a scalar.

2. How can a parallelogram be solved with vectors?

Ans. The vectors should be drawn so that their starting points match. Then add lines to create a full parallelogram. The outcome is the diagonal of the parallelogram measured from the starting point to the opposite vertex.

3. The parallelogram method uses how many vectors?

Ans. The law uses 2 vectors. When the two vectors to be added link their tails to create the two adjacent sides of a parallelogram, the parallelogram law of vector addition is employed to add the two vectors. The parallelogram's diagonal is then used to calculate the sum of the two vectors.

4. What are the major causes of the Gravesand's apparatus experiment's inaccuracy?

Ans. (1) One of the sources of inaccuracy is friction in the pulleys.

(2) The weights of the threads.

5. What steps may be taken to reduce friction?

Ans. The pulleys should be lubricated to reduce friction.

6. Why are the weights hanging off the board or table instead of being fastened to them?

Ans. So that the response of the board or table does not change its effective weight.

7. What do rectangular components actually look like?

Ans. The two vector components perpendicular to one another are known as rectangular (or right angle) components.

8. What are the parallelogram's five fundamental laws?

Ans. The characteristics of parallelograms: 

• Congruent sides are opposite sides (AB = DC).

• Congruent opposite angles (D = B) exist.

• Angles that are adjacent are supplementary (A + D = 180°).

• All angles are correct if one angle is correct.

• A parallelogram's diagonals cut through one another.

9. What is the name of unit vectors?

Ans. A vector is a unit of measurement with both magnitude and direction. A unit vector is a vector with a magnitude 1. Another name for it is Direction Vector

10. How do you multiply numerical values by a vector?

Ans. When vectors are multiplied by positive values, their directions remain unchanged, but their magnitudes change. However, the magnitude and direction of a vector are altered when multiplied by a negative value. 

Practical Based Questions

1. If P>Q and P and Q act in opposite directions but along the same straight line, then what is the outcome?

1. P+Q

2. P-Q

3. P/Q

4. Q/P

Ans. B) The outcome is P-Q

\[{\rm{S = }}\sqrt {\left( {{P^2} + {Q^2} + 2PQ{\rm{Cos}}\theta } \right)} \]

\[\theta  = {180^\circ }\]

\[{\rm{S = }}\sqrt {\left( {{P^2} + {Q^2} + 2PQ{\rm{Cos}}{{180}^\circ }} \right)} \]

\[{\rm{S = }}\sqrt {\left( {{P^2} + {Q^2} - 2PQ} \right)} \]

\[{\rm{S = }}\sqrt {{{(P - Q)}^2}} \]

\[S = P - Q\]

2. When two equal forces P combine to form an angle of, the outcome is:

1. \[2P{\rm{Sin}}\dfrac{\theta }{2}\]

2. \[2P\tan \dfrac{\theta }{2}\]

3. \[2P{\rm{Cos}}\dfrac{\theta }{2}\]

4. \[2PCot\dfrac{\theta }{2}\]

Ans.  B) \[2P{\rm{Cos}}\dfrac{\theta }{2}\]

\(\begin{array}{l}R = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}\cos \theta } \\F1 = F2\\R = \sqrt {{P^2} + {P^2} + 2P.P\cos \theta } \\R = \sqrt {2{P^2}(1 + 2\cos \theta )} \\R = \sqrt {2{P^2}(2{{\cos }^2}\dfrac{\theta }{2})} \\R = 2P\cos \dfrac{\theta }{2}\end{array}\)

3. When the resultant is maximum and minimum, the angle between the two forces is: 

1. \[{0^\circ },{180^\circ }\]

2. \[{90^\circ },{180^\circ }\]

3. \[{180^\circ },{90^\circ }\]

4. \[{90^\circ },{0^\circ }\]

Ans.  A)The angle between the two forces is \[{0^\circ },{180^\circ }\].

4. The product of two equal right-angled forces, each equal to P, is:

1. \[\dfrac{P}{2}\]

2. \[\dfrac{P}{{2\sqrt 2 }}\]

3. \[\dfrac{P}{{\sqrt 2 }}\]

4. \[\sqrt 2 P\]

Ans. D) \[\sqrt 2 P\]

\[{\rm{S = }}\sqrt {\left( {{P^2} + {Q^2} + 2PQ{\rm{Cos}}\theta } \right)} \]

\[{\rm{S = }}\sqrt {\left( {{P^2} + {Q^2} + 2PQ{\rm{Cos}}90} \right)} \]

\[{\rm{S = }}\sqrt {\left( {{P^2} + {P^2}} \right)} \]

\[{\rm{S = }}\sqrt {\left( {2{P^2}} \right)} \]

\[S = \sqrt 2 P\]

5. What we call the one force that may affect an item as effectively as multiple separate forces.

1. Resultant Force

2. Parallelogram Force

3. Diagonal Force

4. Reduced Force

Ans. A) Resultant Force is the one force that may affect an item as effectively as multiple separate forces.

6. Who established the parallelogram law for adding forces?

1. Isaac Newton

2. Galileo

3. Johannes Kepler

4. Albert Einstein

Ans. A) Issac Newton established the parallelogram law for adding forces.

7. According to the Parallelogram Law of Forces, if two forces acting simultaneously on a particle are represented in magnitude and direction by two adjacent sides of a parallelogram, their results may be described by?

1. The parallelogram's diagonal that runs through the points where the forces intersect

2. The parallelogram's diagonal that does not cut through the forces' junction point

3. it’s a shorter side

4. Its longer side

Ans. A) The results may be described in magnitude and direction by the parallelogram's diagonal that runs through the points where the forces intersect.

8. According to the triangle law of forces, if two forces acting simultaneously on a particle can be represented in magnitude and direction by the first two sides of a triangle taken in sequence, then their results can be represented in magnitude and direction by the third side of a triangle taken in sequence.

1. True

2. False

Ans.  A) True, if two forces acting simultaneously on a particle can be represented in magnitude and direction by the first two sides of a triangle taken in sequence, then their results can be represented in magnitude and direction by the third side of a triangle taken in sequence.

9. Which of the following is not a force-related effect?

1. An object's direction can be altered by force

2. An object's shape can be altered by force

3. A moving object's speed can be increased by force

4. An object's mass can be decreased through force

Ans. D) An object's mass can be decreased through force.

10. How much does a 60 kg boy weigh on the moon?

1. 10 kg -f

2. 6 kg-f

3. 1/6 kg-f

4. Zero N

Ans. A) 10 kg-f

weight on moon= weight on earth/6kg

Conclusions

The Parallelogram law of vector addition states that if the adjacent sides of a parallelogram can represent two vectors in magnitude and direction, then the results can be represented by the parallelogram's diagonal in magnitude and direction. The examination and observation can be done using Gravesand's apparatus.