
What is the z-score for a 98% confidence interval?
Answer
531k+ views
Hint: For solving this type of questions, you should know how to read the standard normal probabilities table. You have to check it carefully for your values. You should find your value or the nearest value of the value you find after getting the confidence $\left( 1-x \right)g100\%$ . We should get the significance before this and then get the critical value.
Complete step by step answer:
In our question it is given that we have to find the z-score $\left( z* \right)$ for the confidence interval of 98%. So, first we have to mark 98% on the graph and then we have to find the tail.
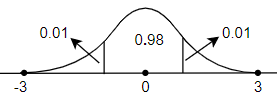
For the tail point of both the tails,
$1-0.98=0.02$
For the tail point of single tail,
$\dfrac{0.02}{2}=0.01$
So, now the values are:
Now, we will use the formula for confidence, that is,
$\left( 1-x \right)g100\%=98\%$
Here, we know, significance is,
$x=0.02$
And then with the help of significance we will be calculating critical value, that is, ${{z}_{x/2}}$.
We will now find 0.01 in the ‘df’ row at the top of page $A_{12}$. ${{z}_{x/2}}$ is the last entry in the column under 0.01. The table is given as below.
Hence ${{z}_{x/2}}=2.326$ for 98% confidence.
So, by reading the values in the table and solving this, we get that the z-score of a 98% confidence interval is 2.326.
Note: If your significance value is any value and we by dividing it, we get the values of the tails. And then we check this value in the table or ‘df’ row and if our same value is not available in the table, then we take the nearest value in the table and use the just greater value for getting the answer.
Complete step by step answer:
In our question it is given that we have to find the z-score $\left( z* \right)$ for the confidence interval of 98%. So, first we have to mark 98% on the graph and then we have to find the tail.

For the tail point of both the tails,
$1-0.98=0.02$
For the tail point of single tail,
$\dfrac{0.02}{2}=0.01$
So, now the values are:
Now, we will use the formula for confidence, that is,
$\left( 1-x \right)g100\%=98\%$
Here, we know, significance is,
$x=0.02$
And then with the help of significance we will be calculating critical value, that is, ${{z}_{x/2}}$.

We will now find 0.01 in the ‘df’ row at the top of page $A_{12}$. ${{z}_{x/2}}$ is the last entry in the column under 0.01. The table is given as below.
| z | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 |
| 0.5 | 0.2088 | 0.2123 | 0.2157 | 0.2190 | 0.2224 |
| 0.6 | 0.2422 | 0.2454 | 0.2486 | 0.2517 | 0.2549 |
| 0.7 | 0.2734 | 0.2764 | 0.2794 | 0.2823 | 0.2852 |
| 0.8 | 0.3023 | 0.3051 | 0.3078 | 0.3106 | 0.3133 |
| 0.9 | 0.3289 | 0.3315 | 0.3340 | 0.3365 | 0.3389 |
| 1.0 | 0.3531 | 0.3554 | 0.3577 | 0.3599 | 0.3621 |
Hence ${{z}_{x/2}}=2.326$ for 98% confidence.
So, by reading the values in the table and solving this, we get that the z-score of a 98% confidence interval is 2.326.
Note: If your significance value is any value and we by dividing it, we get the values of the tails. And then we check this value in the table or ‘df’ row and if our same value is not available in the table, then we take the nearest value in the table and use the just greater value for getting the answer.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Explain zero factorial class 11 maths CBSE

What organs are located on the left side of your body class 11 biology CBSE

Draw a diagram of nephron and explain its structur class 11 biology CBSE

How do I convert ms to kmh Give an example class 11 physics CBSE




