Question

You are downloading a song. The percent $y$ (in decimal form) of megabytes remaining to get downloaded in $x$ seconds is given by $y = - 0.1x + 1$. Solve the following questions:
 (1) Draw the graph of the function.
(2) Find the total MB of the song.
(3) After how many seconds will 75% of the song get downloaded?
(4) After how many seconds the song will be downloaded completely?

Answer 1

Hint: The downloading equation given in the question is $y = - 0.1x + 1$. This equation suggests that the amount left to be downloaded is varying linearly with time. Thus this is a straight line equation with negative slope. Compare it with the general equation to draw the graph. Put the values given in the question to find the time after which 75% and 100% of the song will be completed.

Complete step-by-step solution:
According to the question, while downloading a song, the percentage left to download is given by the equation as:
$ \Rightarrow y = - 0.1x + 1$
(1) This equation is a straight line equation with negative slope. If we compare it with the general equation of straight line $y = mx + c$, we have:
$ \Rightarrow m = - 0.1{\text{ and }}c = 1$
Using these information, the graph is as shown below:

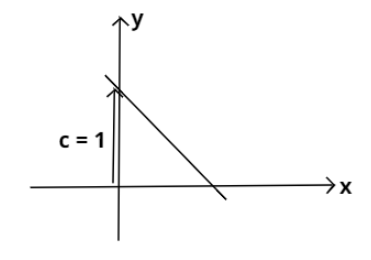
$c$ is representing the $y$ intercept.
(2) Here we have to calculate the total MB of the song.
The downloading equation $y = - 0.1x + 1$ is given in percentage terms. $y$ is the percentage (in decimal) of the song remaining to be downloaded and $x$ is time in seconds. But there is nowhere any information given about the number of MB which is already downloaded at any instant or the number of MB which is left to be downloaded at any instant.
The entire data is given in percentage terms. So the absolute value of the total number of MB of the song can’t be determined.
(3) We have to determine after how many seconds 75% of the song will be downloaded.
The downloading equation $y = - 0.1x + 1$ is given in percentage terms. $y$ is the percentage (in decimal) of the song remaining to be downloaded and $x$ is time in seconds.
If 75% of songs are downloaded, it means 25% is left to be downloaded. Thus we put $y = 25\% = 0.25$ ($y$ is in decimal terms) in the equation, we’ll get:
$
   \Rightarrow 0.25 = - 0.1x + 1 \\
   \Rightarrow 0.1x = 0.75 \\
   \Rightarrow x = 7.5{\text{ sec}}
 $
Thus 75% of the song will be downloaded in 7.5 seconds.
(4) Here we have to determine the time after which the song will be completely downloaded.
If 100% of the song is downloaded already, the percentage left to be downloaded is 0. Thus we put $y = 0$ in the same equation, we’ll get:
$
   \Rightarrow 0 = - 0.1x + 1 \\
   \Rightarrow 0.1x = 1 \\
   \Rightarrow x = 10{\text{ sec}}
 $
The song will be completely downloaded in 10 seconds.

Note: In the second part of the above question, if some data was given like after $a$ seconds $k$ MB of song is already downloaded or after $b$ seconds $p$ MB of song is left to be downloaded, we would have calculated the exact total MB of the song.
But there was no such data and the equation is given in percentage that’s why we can’t calculate the total MB of the song.