Question

A moving boat is observed from the top of a 150 m high cliff moving away from the cliff. The angle of depression of the boat changes from ${{60}^{0}}$ to ${{45}^{0}}$ in 2 minutes. Find the speed of the boat in m/h.

Answer 1

Hint: For solving this problem first we will draw the geometrical figure as per the given data. After that, we will use the basic formula of trigonometry $\tan \theta =\dfrac{\left( \text{length of the perpendicular} \right)}{\left( \text{length of the base} \right)}$ . Then, we will find the distance travelled by the boat in 2 minutes and use the formula $\text{Speed}=\dfrac{\text{Distance}}{\text{Time}}$ to find the speed of the boat easily.
Complete step-by-step answer:
Given:
It is given that a moving boat is observed from the top of a 150 m high cliff moving away from the cliff. The angle of depression of the boat changes from ${{60}^{0}}$ to ${{45}^{0}}$ in 2 minutes. And we have to find the speed of the boat in m/h.
Now, first, we will draw a geometrical figure as per the given data. For more clarity look at the figure given below:

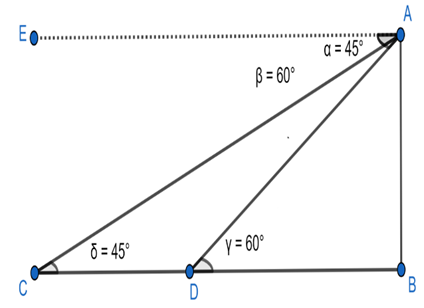
In the above figure, AB represents the 150 m high cliff. Initially, the boat is at point D and it moves to point C in 2 minutes. And as it is given that The angle of depression of the boat changes from ${{60}^{0}}$ to ${{45}^{0}}$ so, $\alpha =\angle CAE={{45}^{0}}$ and $\beta =\angle DAE={{60}^{0}}$ .
Now, as EA is parallel to the line CB and we know that alternate interior angles are equal. Then,
$\begin{align}
  & \angle ACB={{45}^{0}} \\
 & \angle ADB={{60}^{0}} \\
\end{align}$
Now, we consider $\Delta ADB$ in which $\angle ABD={{90}^{0}}$ , $AB=150$ is the length of the perpendicular, DB is the length of the base and $\angle ADB={{60}^{0}}$ . Then,
$\begin{align}
  & \tan \left( \angle ADB \right)=\dfrac{\left( \text{length of the perpendicular} \right)}{\left( \text{length of the base} \right)} \\
 & \Rightarrow \tan {{60}^{0}}=\dfrac{AB}{DB} \\
 & \Rightarrow \sqrt{3}=\dfrac{150}{DB} \\
 & \Rightarrow DB=\dfrac{150}{\sqrt{3}} \\
 & \Rightarrow DB=50\sqrt{3}.........................\left( 1 \right) \\
\end{align}$
Now, we consider $\Delta ACB$ in which $\angle ABC={{90}^{0}}$ , $AB=150$ is the length of the perpendicular, CB is the length of the base and $\angle ACB={{45}^{0}}$ . Then,
$\begin{align}
  & \tan \left( \angle ACB \right)=\dfrac{\left( \text{length of the perpendicular} \right)}{\left( \text{length of the base} \right)} \\
 & \Rightarrow \tan {{45}^{0}}=\dfrac{AB}{CB} \\
 & \Rightarrow 1=\dfrac{150}{CB} \\
 & \Rightarrow CB=150........................\left( 2 \right) \\
\end{align}$
Now, as we know that points C, D and B lies on the same line segment. Then,
$\begin{align}
  & CB=CD+DB \\
 & \Rightarrow CD=CB-DB \\
\end{align}$
Now, put $CB=150$ from equation (2) and $DB=50\sqrt{3}$ from equation (1) into the above equation. Then,
$\begin{align}
  & CD=CB-DB \\
 & \Rightarrow CD=150-50\sqrt{3} \\
 & \Rightarrow CD\approx 150-86.6025 \\
 & \Rightarrow CD=63.3975 \\
\end{align}$
Now, as it is given that the boat covers CD distance in 2 minutes. And we know that there are 60 minutes in 1 hour. Then,
$2\text{ minutes = }\dfrac{2}{60}\text{ hour}$
Now, as we know that speed is equal to distance divided by time. Then,
Speed of the boat $=\dfrac{CD}{\dfrac{2}{60}}=63.3975\times 30=1901.925$ m/h.
Now, as we know that there are 1000 metres in 1 Km. Then,
Speed of the boat $=1901.925$ m/h $=\dfrac{1901.925}{1000}\approx 1.9$ Km/h.
Now, we conclude that the speed of the boat will be $1901.925$ m/h or $1.9$ Km/h approximately.

Note: Here, the student should first try to understand what is asked in the problem. After that, we should try to draw the geometrical figure as per the given data and proceed stepwise and, while making the figure we should remember that angle of depression of the bot from the top of the cliff is given. Moreover, we should apply the basic formula of trigonometry properly without any error and avoid calculation mistakes while solving to get the correct answer.