
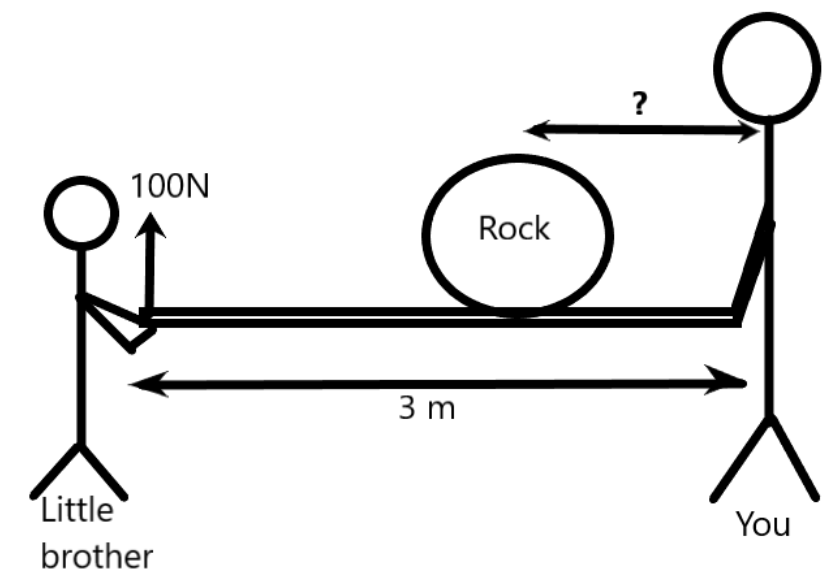
You and your little brother are shifting a large 58kg rock by carrying it together on a 3.0m long litter as shown in the figure. Your little brother is capable of exerting an upward force of 100N on one end of the litter. How far should the rock be placed from you in order for you and your brother to carry the litter without it tipping? (in standard form)

Answer
564.6k+ views
Hint: We are given a situation in which the weight from a rock should be balanced between two people carrying it on a litter at two ends such that there is no chance of tipping. We can use the torque conditions for knowing the unknown parameter.
Complete step-by-step solution:
We know that torque is the rotational quantity of the force applied to a system, which has a tendency to rotate. In our given situation, the heavy rock is being carried by two unequal forces on a litter.
The younger brother is capable of 100N force in the vertical direction. We know that the mass of the rock is 58kg, i.e., 580N weight, therefore, the weight to be applied by you should be the difference in these two given by –
\[\begin{align}
& {{F}_{you}}=580N-100N \\
& \Rightarrow {{F}_{you}}=480N \\
\end{align}\]
Now, let us consider the situation when the rock can tip off the litter. The net torque on it will not be equal. So, we need the condition when the net torque acting on the rock due to the two lifters are equal.
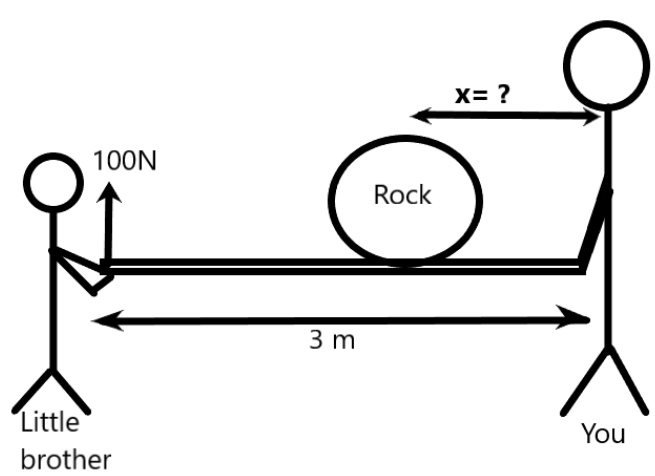
For that, let us consider ‘x’ as the distance from you to the rock. The product of the force applied by you and the distance will give the torque due to your force. Similarly, we can find the torque for your little brother also. We need both of them to be equal to avoid the tipping of the rock.
i.e.,
Torque due to you is given as –
\[{{\tau }_{you}}={{F}_{you}}\times x\]
Torque due to the little brother is given as –
\[{{\tau }_{bro}}={{F}_{bro}}\times (3-x)\]
Now, we can equate the above two torque values as –
\[\begin{align}
& {{\tau }_{you}}={{\tau }_{bro}} \\
& \Rightarrow {{F}_{you}}x={{F}_{bro}}(3-x) \\
& \Rightarrow 480x=100(3-x) \\
& \Rightarrow 480x=300-100x \\
& \Rightarrow 580x=300 \\
& \therefore x=0.517m \\
\end{align}\]
We get the distance ‘x’ from you to the position of the rock to be 0.517m.
In standard form,
\[x=5.17\times {{10}^{-1}}m\]
When the rock is kept at 0.52m away from you, the rock doesn’t tip. This is the required solution.
Note: The above problem signifies the role of distance in handling heavy objects. The lever system which is used in lifting weights uses this technique to easily carry heavy objects in the air with comparatively very less force applied by the worker on the other side.
Complete step-by-step solution:
We know that torque is the rotational quantity of the force applied to a system, which has a tendency to rotate. In our given situation, the heavy rock is being carried by two unequal forces on a litter.

The younger brother is capable of 100N force in the vertical direction. We know that the mass of the rock is 58kg, i.e., 580N weight, therefore, the weight to be applied by you should be the difference in these two given by –
\[\begin{align}
& {{F}_{you}}=580N-100N \\
& \Rightarrow {{F}_{you}}=480N \\
\end{align}\]
Now, let us consider the situation when the rock can tip off the litter. The net torque on it will not be equal. So, we need the condition when the net torque acting on the rock due to the two lifters are equal.
For that, let us consider ‘x’ as the distance from you to the rock. The product of the force applied by you and the distance will give the torque due to your force. Similarly, we can find the torque for your little brother also. We need both of them to be equal to avoid the tipping of the rock.
i.e.,
Torque due to you is given as –
\[{{\tau }_{you}}={{F}_{you}}\times x\]
Torque due to the little brother is given as –
\[{{\tau }_{bro}}={{F}_{bro}}\times (3-x)\]
Now, we can equate the above two torque values as –
\[\begin{align}
& {{\tau }_{you}}={{\tau }_{bro}} \\
& \Rightarrow {{F}_{you}}x={{F}_{bro}}(3-x) \\
& \Rightarrow 480x=100(3-x) \\
& \Rightarrow 480x=300-100x \\
& \Rightarrow 580x=300 \\
& \therefore x=0.517m \\
\end{align}\]
We get the distance ‘x’ from you to the position of the rock to be 0.517m.
In standard form,
\[x=5.17\times {{10}^{-1}}m\]
When the rock is kept at 0.52m away from you, the rock doesn’t tip. This is the required solution.
Note: The above problem signifies the role of distance in handling heavy objects. The lever system which is used in lifting weights uses this technique to easily carry heavy objects in the air with comparatively very less force applied by the worker on the other side.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Class 11 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Trending doubts
10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Explain zero factorial class 11 maths CBSE

What is a periderm How does periderm formation take class 11 biology CBSE




