
When \[x\le 2,f\left( x \right)=2x+3\] here \[f\left( x \right)\] is a polynomial function, therefore it is continuous on R, in particular it is continuous when \[x\le 2\] .
When \[x>2,f\left( x \right)=2x-3\] here \[f\left( x \right)\] is a polynomial function, therefore it is continuous on R, in particular it is continuous when \[x>2\] at \[x=2\] .
Answer
561k+ views
Hint: For, \[x\le 2,f\left( x \right)=2x+3\] and for \[x>2,f\left( x \right)=2x-3\] . Here, our function is \[f\left( x \right)=\left\{ \begin{align}
& 2x+3,x\le 2 \\
& 2x-3,x>2 \\
\end{align} \right\}\] . Calculate the limit value just before and just after \[x=2\] . If the limit value exists, then the function is said to be continuous.
Complete step by step answer:
According to the question, we are given two cases for the polynomial \[f\left( x \right)\] .
In the \[{{1}^{st}}\] case, we have
When \[x\le 2,f\left( x \right)=2x+3\] here \[f\left( x \right)\] is a polynomial function, therefore it is continuous on R, in particular it is continuous when \[x\le 2\] .
Here, we have \[f\left( x \right)=2x+3\] for all real values of x less than or equal to 2.
Let us plot the function \[f\left( x \right)=2x+3\] on the coordinate axes for all real value of x less than or equal to 2.
\[f\left( x \right)=2x+3,x\le 2\] ……………………………………(1)
We can observe that the function \[f\left( x \right)\] is a straight line with slope equal to 2 and y intercept equal to 3.
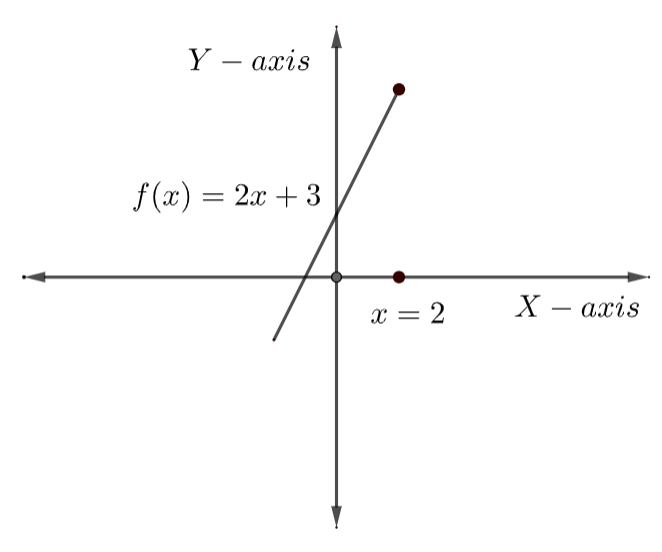
In the \[{{2}^{nd}}\] case, we have
When \[x>2,f\left( x \right)=2x-3\] here \[f\left( x \right)\] is a polynomial function, therefore it is continuous on R, in particular it is continuous when \[x>2\] at \[x=2\] .
Here, we have \[f\left( x \right)=2x-3\] for all real values of x greater than 2.
Let us plot the function \[f\left( x \right)=2x+3\] on the coordinate axes for all real value of x greater than 2.
\[f\left( x \right)=2x-3,x>2\] ……………………………………(2)
We can observe that the function \[f\left( x \right)\] is a straight line with slope equal to 2 and y intercept equal to -3.
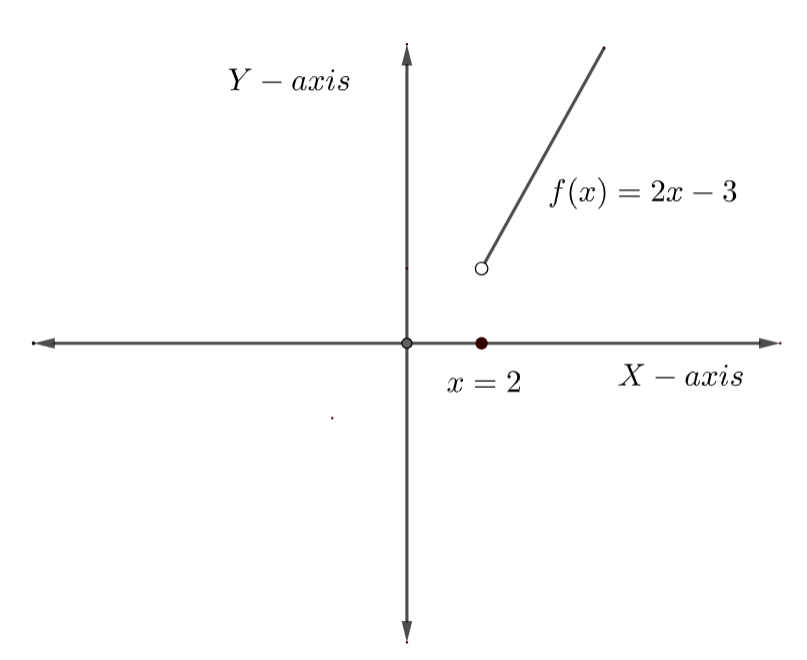
In the above diagram we can observe that there is open dot at \[x=2\] . It means the function \[f\left( x \right)\] doesn’t take the value \[f\left( x \right)=2x-3\] at \[x=2\] .
On combining equation (1) and equation (2), we get
\[f\left( x \right)=\left\{ \begin{align}
& 2x+3,x\le 2 \\
& 2x-3,x>2 \\
\end{align} \right\}\]
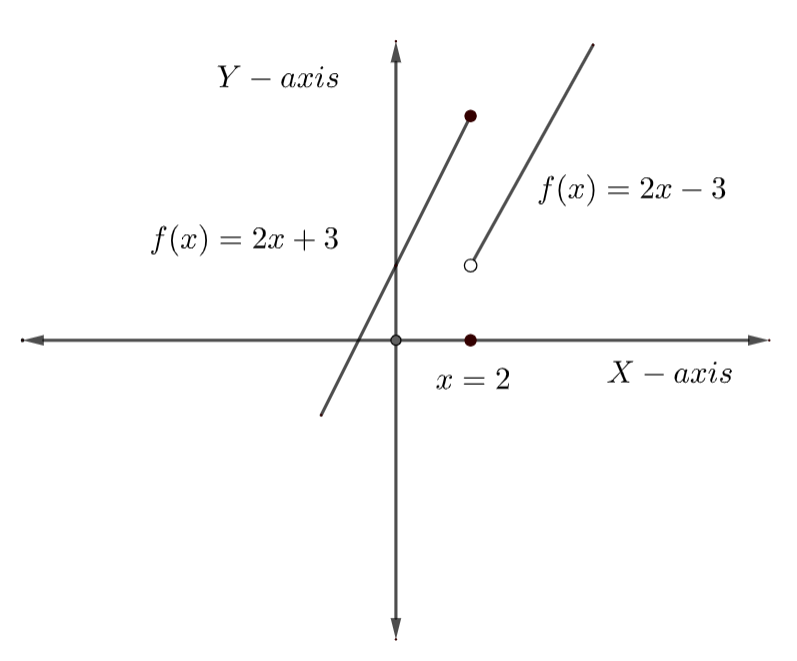
For the function, to be continuous, the limit must exist at \[x=2\] .
For \[x=2+h\] where \[h\to 0\] , we have
\[\displaystyle \lim_{h\to 0}2\left( 2+h \right)-3=4-3=1\] …………………………………………..(3)
Similarly, for \[x=2-h\] where \[h\to 0\] , we have
\[\displaystyle \lim_{h\to 0}2\left( 2-h \right)+3=4+3=7\] ……………………………………………..(4)
Now, from equation (3) and equation (4), we have the limit value just before and just after \[x=2\] .
Therefore, the given function is continuous.
Note: In this type of question, where we are asked to check the continuity of the function at a specific point. The best way to approach this type of question is to find the value of the limit just before and just after that point. If the value of the limit exists then, the function is said to be continuous.
& 2x+3,x\le 2 \\
& 2x-3,x>2 \\
\end{align} \right\}\] . Calculate the limit value just before and just after \[x=2\] . If the limit value exists, then the function is said to be continuous.
Complete step by step answer:
According to the question, we are given two cases for the polynomial \[f\left( x \right)\] .
In the \[{{1}^{st}}\] case, we have
When \[x\le 2,f\left( x \right)=2x+3\] here \[f\left( x \right)\] is a polynomial function, therefore it is continuous on R, in particular it is continuous when \[x\le 2\] .
Here, we have \[f\left( x \right)=2x+3\] for all real values of x less than or equal to 2.
Let us plot the function \[f\left( x \right)=2x+3\] on the coordinate axes for all real value of x less than or equal to 2.
\[f\left( x \right)=2x+3,x\le 2\] ……………………………………(1)
We can observe that the function \[f\left( x \right)\] is a straight line with slope equal to 2 and y intercept equal to 3.

In the \[{{2}^{nd}}\] case, we have
When \[x>2,f\left( x \right)=2x-3\] here \[f\left( x \right)\] is a polynomial function, therefore it is continuous on R, in particular it is continuous when \[x>2\] at \[x=2\] .
Here, we have \[f\left( x \right)=2x-3\] for all real values of x greater than 2.
Let us plot the function \[f\left( x \right)=2x+3\] on the coordinate axes for all real value of x greater than 2.
\[f\left( x \right)=2x-3,x>2\] ……………………………………(2)
We can observe that the function \[f\left( x \right)\] is a straight line with slope equal to 2 and y intercept equal to -3.

In the above diagram we can observe that there is open dot at \[x=2\] . It means the function \[f\left( x \right)\] doesn’t take the value \[f\left( x \right)=2x-3\] at \[x=2\] .
On combining equation (1) and equation (2), we get
\[f\left( x \right)=\left\{ \begin{align}
& 2x+3,x\le 2 \\
& 2x-3,x>2 \\
\end{align} \right\}\]

For the function, to be continuous, the limit must exist at \[x=2\] .
For \[x=2+h\] where \[h\to 0\] , we have
\[\displaystyle \lim_{h\to 0}2\left( 2+h \right)-3=4-3=1\] …………………………………………..(3)
Similarly, for \[x=2-h\] where \[h\to 0\] , we have
\[\displaystyle \lim_{h\to 0}2\left( 2-h \right)+3=4+3=7\] ……………………………………………..(4)
Now, from equation (3) and equation (4), we have the limit value just before and just after \[x=2\] .
Therefore, the given function is continuous.
Note: In this type of question, where we are asked to check the continuity of the function at a specific point. The best way to approach this type of question is to find the value of the limit just before and just after that point. If the value of the limit exists then, the function is said to be continuous.
Recently Updated Pages
Why are manures considered better than fertilizers class 11 biology CBSE

Find the coordinates of the midpoint of the line segment class 11 maths CBSE

Distinguish between static friction limiting friction class 11 physics CBSE

The Chairman of the constituent Assembly was A Jawaharlal class 11 social science CBSE

The first National Commission on Labour NCL submitted class 11 social science CBSE

Number of all subshell of n + l 7 is A 4 B 5 C 6 D class 11 chemistry CBSE

Trending doubts
10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




