Question

$
x = \left\{ {21,22,23,24,25,26,27,28,29,30} \right\}\\
A = \left\{ {x:x{\rm{ is a multiple of 3}}} \right\}\\
B = \left\{ {x:x{\rm{ is a prime}}} \right\}\\
C = \left\{ {x:x \le 25} \right\}
$
(a) Complete the Venn diagram.

Answer 1

Hint: Venn diagrams are a set of circles that are used to represent the relationships or the commonalities between a group or number of groups of people or things. In this question a set of numbers is given and these numbers are divided into three sets based on different conditions, these sets are represented by the circles in the Venn diagram. We have to find the numbers that are common among them and then use these numbers to complete this Venn diagram.

Complete step-by-step answer:
Given:
The total set of numbers $x = \left\{ {21,22,23,24,25,26,27,28,29,30} \right\}$
The numbers that belong to set A are given,
$A = \left\{ {x:x{\rm{ is a multiple of 3}}} \right\}$
Multiple of 3 in the total set of numbers are – 21, 24, 27 and 30.
So, the set A has,
$\Rightarrow A = \left\{ {21,24,27,30} \right\}$
Similarly, now the numbers that belong to set B are given,
$B = \left\{ {x:x{\rm{ is a prime}}} \right\}$
The prime numbers in the total set of numbers are – 23 and 29.
So, the set B has,
$\Rightarrow B = \left\{ {23,29} \right\}$
And now, the numbers that belong to set C are given as –
$C = \left\{ {x:x \le 25} \right\}$
The numbers that are less than or equal to 25 in the total set of numbers are – 21, 22, 23, 24 and 25.
So, the set C has,
$\Rightarrow C = \left\{ {21,22,23,24,25} \right\}$
Now, the numbers that are common in both sets A and B are given as –
$
A \cap B = \left\{ {21,24,27,30} \right\} \cap \left\{ {23,29} \right\}\\
 = \left\{ 0 \right\}\\
 = \phi
$
Which means that there are no common numbers in the set $A \cap B$.
Similarly, the numbers that are common in both sets B and C are given as –
$
B \cap C = \left\{ {23,29} \right\} \cap \left\{ {21,22,23,24,25} \right\}\\
 = \left\{ {23} \right\}
$
And now, the numbers that are common in both sets A and C are given as –
$
A \cap C = \left\{ {21,24,27,30} \right\} \cap \left\{ {21,22,23,24,25} \right\}\\
 = \left\{ {21,24} \right\}
$
And finally, the numbers that are common in all the three sets A, B and C are given as –
$
A \cap B \cap C = \left\{ {21,24,27,30} \right\} \cap \left\{ {23,29} \right\} \cap \left\{ {21,22,23,24,25} \right\}\\
 = \left\{ 0 \right\}\\
 = \phi
$
Now we have calculated all the values possible in the Venn diagram, so we can now easily draw the complete Venn diagram.
Therefore, the complete Venn diagram is given below –

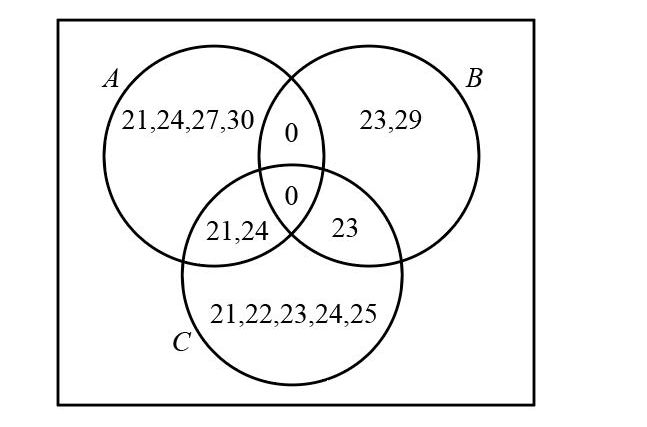
Note: The set $A \cap B$ is read “A intersect B”, which means that it is a set which contains the elements or in this case numbers that are present in both the sets A and B. If any set has zero values in it then this set is known as the “Null Set” or “Empty Set” and this set is represented by $\phi $ symbol. For example, set $A \cap B$ and set $A \cap B \cap C$ are Null sets.